Foreword

Part I

If we assume that all things in nature are discrete, it follows that all things can be described by a finite set of information. This set of information must be accompanied by a process causing it to evolve from one "frame" of time to the next. The most compelling model for meaningful transformation of one finite set of information to another is the computer, and in particular the computer architecture known as "Cellular Automata."

Finite Nature: The hypothesis that all things are discrete rather than continuous; "grainy" rather than "smooth"; step-wise rather than flowing.

Exploring finite quantities

A finite amount of information cannot evolve without a processing mechanism. Information + Process implies a mechanism of computation.

Recapitulation

The Cellular Automaton computer architecture

Part II

Exploring physics as though it were the product of programming run on a computer requires that we explain how the physics of the natural world can be produced by a computer program. Two aspects of physics as we know it -- quantum randomness and reversibility -- are shown to be possible within the framework of familiar computer architecture.

The Universal Computer

Unknowable determinism as an effective source of quantum randomness

Reversibility of the programming.

Part III

The Consequences of Finite Nature

A. The fundamental process that we know as the physics of the natural world is an informational process.

B. Transformation of information is accomplished by a mechanism of computation which is not essentially different from the familiar computers of our technology.

C. The physics of the natural world must be analyzed according to what is necessary and possible for computers to accomplish.

D. There is not, and there need not be, access to the hardware of the Engine from within the program.

Part IV

Information + Process = Computation

Appendix

The Scale of the Simulation

    This paper is an attempt to restate the first of Fredkin's papers, "Finite Nature," as I have understood and appreciated it. I encourage the reader to refer to Fredkin's paper, which is available at http://www.im.lcs.mit.edu/poc/fredkin/Finite-Nature [or http://www.digitalphilosophy.org/finite_nature.htm].

Ross Rhodes
Canton, Ohio
February 8, 2000

If we assume that all things in nature are discrete, it follows that all things can be described by a finite set of information. This set of information must be accompanied by a process causing it to evolve from one "frame" of time to the next. The most compelling model for meaningful transformation of one finite set of information to another is the computer, and in particular the computer architecture known as "Cellular Automata."

Finite Nature: The hypothesis that all things are discrete rather than continuous; "grainy" rather than "smooth"; step-wise rather than flowing.

    The history of science is a progression of discovery in one sense: phenomena once thought to be continuous, flowing, or smooth have been found instead to be discrete, step-like, or grainy. These discoveries are like the close examination of a motion picture: at first it seems to be all smooth motion, but upon inspection it turns out to consist of individual still frames projected at high speed. Or again, it is like looking through a telescope at the entrance leading to a far-off building: at first, the entrance had appeared to be a smooth ramp, but the telescope shows it to be a set of steps.

    Scientific investigation repeatedly has revealed the discrete qualities of nature. We know from high school that all things are made of individual atoms. That is, regardless of whether a substance appears to be solid steel or flowing water or chilly wind, it turns out that all things are made up of discrete, individual molecules and atoms. Similarly, the insubstantial energy of electricity and light has been shown to consist of discrete "chunks," or quanta (from the Latin root which gives us the word "quantity", i.e., a fixed amount ). The hypothetical intrinsic motion of atoms themselves, known as angular momentum, turns out to be "quantized" in discrete units -- existing only in regular and exact "speeds" according to some cosmic gear shift.

    After many years of such investigations, it is now difficult to imagine that any phenomenon of our universe will prove to be continuous in nature.[2] Accordingly, Edward Fredkin's hypothesis of Finite Nature begins with the assumption that all things eventually will be shown to be discrete and, conversely, nothing exists in smooth or continuous form. That is, we assume that all things in nature are finite and limited to their step-like, quantized, discrete units of being.

    In the world of physics, everything must include the basic space and time of our universe. That is to say, Finite Nature assumes that the nothingness and void of empty space will turn out to consist of tiny blocks of length, width and depth; and the flow of time will turn out to consist of motion-picture-like frames of separate instants.

[Top]

    A property or quality which is discrete can be described exactly. For example, if a coin has the discrete property of being heads or tails, then it cannot be anything in between. Accordingly, when we observe that a coin is "heads," we describe the coin's state-of-flip exactly. (If this quality were continuous rather than discrete, the description would always have the flavor of an approximation, owing to the infinite possible rotations of the coin.)

    Where the possible states are so limited, there is an exactly limited amount of description that can be given before we run out of things to describe, and ways to describe them. The state-of-flip (heads or tails) may be one property; and the place-of-minting (Philadelphia, Denver or San Francisco) another; and the denomination (nickel, dime, quarter, etc.) may be another; and so on. Each of these properties, being limited to a certain number of possibilities, can be described with a single choice from among its finite possibilities. Even such seemingly continuous properties as the general condition of the coin are limited to a set of choices -- such as "proof," "mint," "uncirculated," and "circulated" -- rather than being described along a full and infinite range of wear-and-tear. (Although this type of limitation goes against common sense, it is required by Finite Nature and, in fact, it is a good illustration of the baffling step-wise behaviors of quantum mechanics.) We can see that with these restrictions, each coin can be described exactly by stating the value of each property of the coin.

    Given Finite Nature, there are no approximations, no subjective values. A collection of three coins, in our example, can be arranged and rearranged in only a finite number of ways before one runs out of possible combinations. Flipping one or another will yield different state-of-flip arrangements with exactly 8 possibilities, no more and no fewer:[3]

hhh, hht

hth, htt

thh, tht

tth, ttt

Similarly, the possible place-of-minting values will be exactly 27, no more and no fewer:

PPP, PPD, PPS

PDP, PDD, PDS

PSP, PSD, PSS

DPP, DPD, DPS

DDP, DDD, DDS

DSP, DSD, DSS

SPP, SPD, SPS

SDP, SDD, SDS

SSP, SSD, SSS

Choosing to describe both of these properties for our collection of three coins (Ph-Ph-Ph, Ph-Ph-Pt, etc.) increases the number of possibilities in a tidy mathematical way, so that resulting number of possibilities, while large, remains exact and decidedly finite.[4]

    Fredkin's hypothesis of Finite Nature sees this restriction on the amount of information needed to provide a full and complete description of any aspect of physics as the prime implication of the assumption that all things are discrete, step-wise, or grainy. If all of space-time and all physical processes are fundamentally discrete, then for any given unit of space-time (i.e., for any volume of anything, or even a volume of nothing) there will be a limited, finite number of combinations that will describe all of the possible states of everything contained within that volume. Put another way, this is to say that for every volume of space-time there will be a definite and finite amount of information contained within it.

    When Fredkin invokes the concept of "information," he is speaking of a "scalar quantity," that is, something which is "capable of being represented by a point on a scale," or "a quantity that has a magnitude describable by a real number and no direction." These are properties that can be quantified, properties that can be expressed as numbers. How fast? 60 m.p.h. (as opposed to the alternative non-scalar description, "rapidly"). Finite Nature supposes that all properties can be expressed by numbers because all properties are discrete and step-wise. In this sense, Fredkin is referring to the data itself as the relevant information, rather than the meaning associated with the data. Accordingly, the information can as easily be expressed by numbers as by characters, words or sentences. Thus, heads could be represented by "0" and tails by "1", so that heads-heads-tails (or hht) could be represented by "001". The interpretation of these numbers is easily accomplished simply by keeping track of what each digit is supposed to represent.[5]

    To assert that all information in nature consists of scalar quantities is a radical statement. We have become accustomed in mathematics and in the natural world to contemplating the infinite -- a series that goes on forever without end -- and its converse, the infinitesimal -- a hypothetical smallness that has no minimum. The invention of calculus by Newton and Leibnitz provided the mathematical tools for taming the philosophical concepts of the infinite and the infinitesimal. Engineers and scientists, for the most part, have stopped thinking about these concepts as problems because they no longer present any barrier to satisfactory calculation.[6] Consequently, the areas in which these twin concepts are most in conflict with our sensibilities -- the realm of time and space, or simply space-time -- are commonly thought of as continuous because, first, time and space appear to be continuous; second, the mind reels at the contemplation of any alternative; and third, space-time may safely be assumed to be continuous with no loss of function. However, to say that it is convenient to credit the appearance of continuity is not at all to say that space and time actually are continuous. The examples given from atomic theory in chemistry, and quantum theory in physics, serve as reminders that close examination can reveal step-wise, discrete properties at any (and perhaps every) turn. Fredkin supposes that investigation will show that there is no infinite and no infinitesimal; all things in nature and physics are finite.

[Top]

    To this point, Fredkin has been considering the volume of space-time as a static block of information -- a finite block of information in its present state. However, we know from our experience that the properties of the natural world evolve. That is to say, the volume of space-time has a past where its overall state was different, and also a future where its overall state will be different still.

    We may ask how this change can be accomplished. In light of our assumption that time itself is discrete and step-wise, we are not permitted to imagine the information sliding or morphing from one state to the next; no, the information must be in one state in the present moment, and in another, different state in the next succeeding future moment. Moreover, the discrete nature of each separate property must effect a complete change from moment to moment, with no possibility of "transition." From one moment to the next -- from one time-step to the next -- the information must be transformed completely to a new and different, but equally finite, set of information describing the volume of space-time as it then exists.

    This exercise recalls Zeno's paradoxes of motion involving space and time. Zeno argued that motion (i.e., an evolution from one position to the next) is not possible when space and time are discrete qualities.[7] Space is divided into some type of blocks or cells; time is divided into steps marked by ticks of the clock. Accordingly, at any given time step 1, the block or cell exists (by definition) wholly and completely in state 1. The finite amount of information necessary to make a complete description of the space-time unit will not change -- it cannot change, because any change would involve intermediate time steps which, according to our fundamental assumption of Finite Nature, do not exist. Nevertheless, at time step 2, the same block or cell exists in a different state 2! How does such a transformation occur?

    The fact that we observe motion, and other aspects of a system which evolves over time, was the unsolvable problem for Zeno.[8] Fredkin, however, resolves the paradox neatly by reference to a system of apparent motion unknown to the ancient Greeks -- the common operations of a computer program. By reducing the volume of space-time to a symbolic representation of the information contained within it, Fredkin produces the full equivalent of the volume of space-time in the form of the information itself. Thus, three pennies minted in Denver and flipped may be represented as ¢Dh, ¢Dt, ¢Dh. Nothing would be added to this information by using real coins, and we can save a great deal of copper by substituting the symbols.[9] Given Finite Nature, there is literally no difference between the information content of the volume of space-time and the "thing itself" because the information is the thing and vice versa.

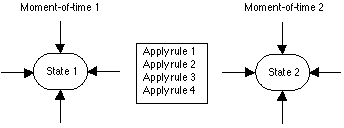
    In order to better understand Finite Nature, Fredkin suggests that we look to examples of simple systems with similar properties. "A digital computer, exclusive of its input and output facilities (with just a processor and memory),[10] has many of the same properties that we find in Finite Nature." Like Finite Nature, a computer begins with one set of information and proceeds to another, different set of information. The computer's progress is always step-wise, running through a series of ritualistic modifications of the information according to a strict set of programming rules. It is the application of the programming rules that effects the change from the present state of the information to the next succeeding future state.

    The computer's information is represented symbolically by the arrangement of binary switches in the computer's memory. The "state" of the computer is the aggregate arrangement of these memory bits. Consequently, when we consider the state of the computer, we must look at the arrangement in static, fixed form as it exists in its initial state and at the end of a step of programming. The arrangement cannot be changing as we consider it, because the "meaning" represented by the state of the computer depends on the relationship of each bit to every other bit. The computer considers the information coded in its "state" and applies its programming rules to that information, changing the arrangement of the memory bits according to the rules. As the memory bits are being changed, the internal arrangement of the computer is in a state of transition. If the process were stopped in the middle of this transitional phase (before all of the rules for this "step" were fully carried out), an observer looking at the arrangement would not be able to extract any meaning. The overall arrangement would be "wrong" because the application of the rules had not been finished. This would be a computer crash.

    To illustrate, suppose the memory bits were soldiers lined up in a row, and the rule was "take two steps forward, then take one step back." The sergeant must give these orders, one at a time, to each individual soldier, and each soldier then must carry out the orders. If we halted the process mid-application, we might see a very ragged line of soldiers because some of them had taken two steps forward and one step back, some of them had only taken two steps forward, and some had not yet moved. On the other hand, if we allowed the rule to be applied fully, we would see a tidy row of soldiers which had neatly advanced one step.

    A computer achieves this tidy progression through a hardware technique called single clock. As Fredkin explains, "Single clock means that when the computer is in a state, a single clock pulse initiates the transition to the next state. After the clock pulse happens, various changes propagate through the computer until things settle down again. Just after each clock pulse the machine lives for a short time in the messy real world of electrical transients and noise. At the points in time just before each clock pulse the computer corresponds exactly to the workings of a theoretical automaton or Finite State Machine."

    The single clock synchronizes the information processing in a computer, so that the programming can be applied in steps. At the tick of the computer's "clock," the programming is applied and the arrangement of the memory bits begins to change. After all memory bits have been affected, the clock tick is finished and the programming rule has been fully applied.

[Top]

    Edward Fredkin's Finite Nature is the assumption that all things are discrete, step-wise and granular, rather than continuous, flowing or smooth. If this is the case, then all natural phenomena can be represented by scalar values -- numbers. Discrete properties can be represented by these scalar values as a finite set of information, and therefore all of nature can be represented by numbers. Because time itself is assumed to be discrete and step-wise, all transitions must take place "off-stage." The representation of the present moment is changed to a different representation of the future moment and then presented as another finite set of information. The model of a finite set of information represented by scalar values, transformed to a new and equally finite set of information, is to be found in the programming processes of an ordinary computer.

[Top]

    Fredkin notes that one particular type of computer architecture provides a full analogy for the concept of discrete blocks of space-time which evolve, both individually and collectively, from moment to moment. This architecture denominates each computing unit as a "cell," which operates as though it were an independent computer with a simple set of programming instructions. Because it is operating independently and automatically, in robot-like fashion according to its rules, the cell is known as an "automaton" as though it were a robot performing its tasks mindlessly. The aggregation of many of these computing cells comprises the "Cellular Automata" computer architecture.

    There is no difference in principle between the individual cellular automaton and any other computer. Both consist of a block of memory which is acted upon by a set of programming instructions. The difference in practical terms is that the cellular automaton operates according to a severely restricted set of instructions (programming), and so requires a comparatively modest amount of memory. With these limitations, we can create a vast number of cellular automata using our finite memory and programming resources. The key to the utility of the cellular automata ("CA") computer architecture is that when we assemble this vast number of simple, independent computing units, they can interact among themselves in breathtakingly complicated ways.

    To illustrate, let us consider two simple cellular automata, side by side, whose only function in life is to display a color -- either blue or green or red. The one and only rule each must follow is that it should ponder the color of the automaton next to it, and take the color which is next in line alphabetically. Thus, if its neighbor is green, it should take the color red; if red, it should take the color blue; if blue, it should take the color green. We can then watch as the situation changes over time (having arbitrarily assigned colors to each automaton to begin with):

Time step	Cell #1        Cell #2	Application of the rule
1:		Blue's neighbor is green, so it will become red; green's neighbor is blue, so it will become (remain) green.
2:		Red's neighbor is green, so it will become (remain) red; green's neighbor is red, so it will become blue.
3:		etc.
4:		etc.
5:		etc.
6:		etc.

. . . and so on. We have a pattern which, in this case, repeats itself every six steps. Exactly the same rule is applied at each time step, but the pattern is slightly complex. It is the interaction among the cellular automata which causes their states to evolve, and to evolve in a way that bears a relationship between past, present and future such that a pattern emerges.

    Cellular Automata theory considers each automaton as a "cell" surrounded by other cells.

    The simplicity of CA architecture gives rise to a vast complexity of interaction which, in turn, produces pleasing patterns of order as the scale increases. An examination of CA architecture shows that it has the potential to model all varieties of interactions in the natural world for, like a cellular automaton, a quantum unit in our world interacts with its neighbors to produce change according to strict mathematical rules which take into account the quantum unit's own discrete, individual state and the impinging states of its neighbors.[12]

    Fredkin concludes: "Given Finite Nature, what we have at the bottom is a Cellular Automaton of some kind." And, because "Automata, Cellular Automata and Finite State Machines are all forms of computers," this is to say that at the bottom of the physics of the natural world, we have a computer of some kind.

Exploring physics as though it were the product of programming run on a computer requires that we explain how the physics of the natural world can be produced by a computer program. Two aspects of physics as we know it -- quantum randomness and reversibility -- are shown to be possible within the framework of familiar computer architecture.

    A famous proof by the mathematician and theorist Alan Turing in the 1930s holds that all common computers are universal in the sense that their functioning is dependent on the software and independent of the hardware. This means that an Intel-based machine (the common desktop PC) can do whatever a Motorola or PowerPC machine (a Macintosh) can do and vice versa. In fact, either of these can do what a Cray supercomputer can do, only they take more memory and more time in which to do it. After the simple logic gates are constructed (there are only three basic logic gates), the abilities of the computer are entirely a function of the programming. Fredkin's student Roger Banks put forth in 1971 a proof that the same is true of the less conventional computer architecture of a cellular automaton. Because all computers (including cellular automata) are universal, and because the engine at the bottom of the physics of the natural world is a computer of some sort, Fredkin concludes that the ultimate computer is universal (because it is a computer, Q.E.D.).

    If the ultimate computer is universal, as it must be, then we should be able to simulate or, more properly, emulate its operations by the correct programming of our own feeble computers (in the way that a good programmer should be able to emulate a Cray supercomputer using a desktop PC). All of physics as we know it should be expressible as a computer program. As Fredkin puts it,

"What cannot be programmed cannot be physics. This is a very important idea. If a process cannot be programmed on a particular universal computer, despite having enough memory and time, then it cannot be programmed on any computer. If we can't program it on an ordinary computer, Finite Nature implies it can't be a part of physics because physics runs on a kind of computer."

[Top]

    One of the most prominent characteristics of the supremely successful theory of Quantum Mechanics is its dependence on (one might say its slavish adherence to) mathematical formalism.[13] This is some evidence in itself that the physics of our world is the product of calculation.[14] However, Quantum Mechanics has heretofore been understood to require for its operation an element of complete randomness, and true randomness is a problem for computers.[15] It generally has been thought that computers are incapable of producing true randomness. Fredkin explains:

"Uncertainty is at the heart of quantum mechanics. Finite Nature requires that we rule out true, locally generated randomness because such numbers would not, in this context, be considered finite. The reason is that there is no way to create, within a computer, a truly random number that is orthogonal to everything in the computer."

    To solve the problem of computer-generated randomness necessary for a satisfactory model of Quantum Mechanics, Fredkin invokes the concept of "unknowable determinism," a term that is at first blush an oxymoron. Determinism implies a set of rules that can be applied to obtain the eventual result; unknowable implies the absence of any method for obtaining the eventual result. Nevertheless, Fredkin posits a situation exhibiting just these two apparently contradictory facets.

    A peculiar aspect of the operations of Quantum Mechanics is that its operations may be influenced not so much by what is known, but by what can be known in principle.[16] With this fine distinction at hand, Fredkin describes the operations of a Cellular Automaton in which there is no slack in the computations. "Every part of space [every cell] is computing its future as fast [as] possible, while information pours in from every direction." The consequence is that there is no shortcut to obtaining the eventual result. Even in principle, and following a deterministic set of rules, a programmer would have no choice but to simulate the operations of the particular cellular automaton, input the initial conditions (which would be the "state" of every cell in the universe of the cellular automaton), and run the program.

    Given these limitations, running the simulation would not obtain the eventual result until after that result had already occurred on the "original" cellular automaton (or, in the very best hypothetical case, at the same time as the result occurs on the original). Predicting a situation which has already occurred (or presently exists) would not satisfy the Quantum Mechanical definition of a state of affairs which can be known in principle. Accordingly, this process whereby the cellular automaton is "computing its future as fast as possible" effectively mimics "the apparent randomness of quantum mechanical processes" and satisfies the condition that the result should be random in the sense that it is unknowable even in principle.

[Top]

    Reversibility has always been a feature of the equations of physics, which run just as well backwards as forwards. We do not notice such reversibility in our world, and this discrepancy has led to much speculation about why our "arrow of time" moves inexorably forward, never backward.[17] In fact, a number of physical theories make use of events (at least on the minute quantum scale) which actually do run backward in time,[18] without impinging on our experience where a broken egg never picks itself off the floor and reconstitutes itself on the kitchen counter.

    If the physics of our universe is capable of time reversal, at least in principle, then it must also be possible, again in principle, to construct a type of computer similarly capable of running its programs backwards. To do so, the computer must never lose any of the information which brought it to its present "state" because that information will be needed when, running in reverse, the computer must be capable of calculating from the present state backwards into "previous" states. Fredkin posits this concept as a law of "conservation of information." Conventional computing cannot achieve this reversibility, since prior states are "dumped" as the program progresses, according to the laws of thermodynamics. Storing all information from all prior states is impracticable. Far better would be a system whereby simply reversing the mechanics of the computer will reverse the flow of information, such that the reversal will lead to the prior state.

    In 1982, Fredkin developed a model of a computer which could achieve perfect reversibility.[19] He did so by imagining the information stored in the computer as being represented by the positions of billiard balls. Recall that information stored in a computer is almost entirely arbitrary so far as its form is concerned. This being the case, we can just as well define a "0" and a "1" as being the physical positions of a light switch (on or off), or the states of a transistor, or the positions of a billiard ball on the table. The advantage of the billiard ball computer is that the billiard ball changes direction when it collides (interacts) with another ball, or when it collides with a bumper. Because we can imagine a billiard ball hitting a bumper head-on and reversing its direction, a computer constructed of billiard balls has just the desired quality of perfect reversibility.[20]

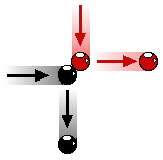
"Particles remember by existing, communicate by moving and compute by interacting." These billiard balls are computing by colliding (interacting), which changes the information about their position and direction of motion. If we could instantaneously reverse the direction of their motion, it is easy to see that they would collide again and regain their former positions (and continue on from there, in reverse, through all prior collisions).

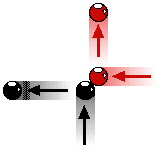
No information is lost in this arrangement, because all of the information that ever existed will recreate itself in the collisions that will continue to occur as all of the billiard balls are thrown into reverse. Accordingly, it is entirely possible, in principle, to compute in a time-reversible fashion. (A good explanation and java demonstration of this concept may be found at What is a Billiard Ball Computer? by James Lin.)

    Fredkin's final point anticipates the second of his seminal papers on this subject, "A New Cosmogony," by introducing the concept of the parts of the model which by their nature are not themselves contained within physics, and so are not to be found in this universe.

[Top]    A. The fundamental process that we know as the physics of the natural world is an informational process.
1. [3.] The most fundamental stuff of physics is not the cells and bits. It is the result of the fundamental process run in the cells with the bits.

2. [7.] Information must have a means of its representation. If we had the right kind of magic microscope, we should always be able to see the digits that represent whatever information is present. Information is never "just there".[22]

3. [16.] Physics is a consequence of the fundamental bits being engaged in the fundamental informational process.

[Top]    B. Transformation of information is accomplished by a mechanism of computation which is not essentially different from the familiar computers of our technology.
4. [4.] The future is computed as a function of the present and (most likely) the past. One way or another, it is very likely a second order system.

5. [1.] The fundamental process that underlies physics must be computation universal. Since the test of a computation universal process is that one can program up a universal machine within it, the existence of computers proves that the fundamental process is universal.

6. [8.] What cannot be programmed cannot be physics. This is a very important idea. If a process cannot be programmed on a particular universal computer, despite having enough memory and time, then it cannot be programmed on any computer. If we can't program it on an ordinary computer, Finite Nature implies it can't be a part of physics because physics runs on a kind of computer.

7. [17.] The Engine is the computer that runs the fundamental informational process that runs physics.

8. [18.] The Engine and the fundamental informational process are computation universal.

9. [19.] Any universal Engine will do (given enough memory).

10. [20.] Physics is totally independent of the characteristics of the engine, so long as it is universal.

[Top]    C. The physics of the natural world must be analyzed according to what is necessary and possible for computers to accomplish.
11. Momentum. [2.] Things don't just happen; everything is a simple consequence of the fundamental process. Viewed from the informational perspective, the idea that a particle just has a momentum makes no sense. If the momentum is reasonably precise, meaning that it is one of a large number of possible momenta, then it contains a substantial amount of information, and that information must have a means of its representation.

12. Inertia. [5.] Matter has inertia because [there must be] some kind of process (like from a field) to change the momentum information (the information that governs the motion of the particle).

13. Accelleration. [6.] A particle accelerates when the environmental information, representing a field or a photon, interacts to change the information associated with the motion of the particle.

14. Yes, Virginia, there is an aether (a reference metric). [10.] Energy, time, spin and other properties of the world cannot be programmed (made to work in an automata) without the existence of a metric.

15. More about the reference metric. [9.] An informational process cannot represent motion without a reference metric; finite nature demands the existence of a metric. This is a difficult idea. The implication is that the computational substrate of quantum mechanics must have access to some kind of metric in order to create inertial motion. Whether or not higher level processes in physics can access that metric is another question. It is hard to see why such access need be forbidden, since every particle must access the metric in order to move. Of course it is also clear that experiments done so far fail to detect any such metric. The argument for asserting the metric is that inertial motion requires an informational process that can take information that represents the velocity and use it to change the position of the particle. There must be information available that allows the process to know the velocity relative to something (the metric) that persists throughout the space that the particle will travel through. Without access to a constant, fixed space-time metric or its informational equivalent, there is no way to create an informational process that can involve particles moving independently in rectilinear motion

16. Quantum randomness. [11.] Digital Mechanics is deterministic with unknowable determinism. [12.] In general, physics is computing the future as fast as it can.

18. Prediction on the macroscopic ("classical") scale. [13.] Some special cases (like the motion of the planets) can be computed faster than physics, allowing for predictions.[23]

19. Prediction on the microscopic ("quantum") scale. [14.] Most microscopic things, like quantum mechanics, cannot be computed on an ordinary computer faster than real time. From our perspective, the information bath that all events are immersed in will always be beyond our computing (in general). Thus, we call events dependent on that information "random".

20. The availability of shortcuts to prediction. [15.] The speed up theorem limits the detail with which we can know the future.

[Top]    D. There is not, and there need not be, access to the hardware of the Engine from within the program.
21. [21.] Everything mentioned in items 1 through 20 above that is in italics [i.e., the computer or engine that runs the fundamental informational process of physics; and the fundamental cells with their memory and bits which are intrinsic to the engine), is not a part of physics and is not to be found in this universe. Rather, it is stuff that exists somewhere, where, perhaps, the rules may be different. If we imagine using a computer to simulate air flow in a wind tunnel, we can think of that simulated airflow as a little universe following simple laws of physics. The computer is not made up of the air flowing in the simulated wind tunnel; the computer is not in the simulated wind tunnel, it is somewhere else.

    Cloning a tree (as growing a tree from a seed) depends on the pre-existence of a store of information constituting a blueprint or map of the eventual tree. The design of the whole tree exists in the genetic material of the single cell -- no matter that the cell may come from the root or the bark or the leaf. Thus, the first fundamental property of an evolving system is structured information.

    To explore the concept further, Fredkin asks why one cannot "clone" a Boeing 747 from scrapings taken from one of the passenger seats. The first answer is that a scraping of vinyl does not contain the blueprint of a 747; it might as well have been scraped from a Chevy Nova or a sofa in the den or any other bit of vinyl. It is not connected, in any informational sense, with a 747. There is no way, even in principle, to discern a Boeing 747 in a scraping of vinyl.

    Suppose, then, that we begin with the blueprint of a Boeing 747 (or a microchip or any other manufactured product) contained on a floppy disk. There is a method, in principle, for converting this information into a full-blown 747: we can at least conceive of a computer-controlled assembly line which would gather the raw materials, forge the parts, and assemble the airplane. Does it follow, then, that we can immerse the floppy disk in a nourishing solution of iron and magnesium and copper and petroleum and ceramics and all of the other organic and inorganic compounds found in a 747, and sit back and watch an airplane grow in the tank? It does not follow. The floppy disk would be ruined.

    We see that an evolving system must begin with information -- whether in DNA strings or on a floppy disk or otherwise -- and that information must be matched to a process suitable for transforming the information into the final structure. For seeds, the process is self-replication, requiring an environment containing the elements found within the cell itself. For blueprints of mechanical systems, stored on floppy disks, the far clumsier process is a computer capable of reading and understanding the stored information, and acting upon it with all manner of ancillary manufacturing systems.

    Accordingly, we begin with information in a digital state. (The genetic material of a tree or other living cell satisfies this definition through its molecular arrangement, which is not different in principle from any other data array.) We must then match the information to a process which will act upon the information and transform it into its eventual, future state.

    Information matched to a transformative process. This is the recipe for development. It is also a fair description of the workings of a computer, in particular a cellular automaton. Given Finite Nature, it is ultimately a description of nature as physics has come to understand it. To Fredkin, this convergence is more than a curiosity: it is an insight into the fundamental workings of our world. Finite Nature means that our world operates as though it were the product of a computing system, and Fredkin sees that this is because our universe is an artifact produced by a computer of some sort.

Canton, Ohio
February 8, 2000

    In the course of his paper "Finite Nature," Fredkin addresses the question that must occur to every physics student: "How small are these cells of which you speak?" The question itself is somewhat misplaced, since it implies physical cells bouncing around in space. Such a concept is the antithesis of Finite Nature, which posits the most fundamental unit as a processing unit, a bit of information, a "virtual computer" or subroutine.

    We might imagine asking, "How small (or large) is Windows98(TM)?" It would be nonsensical to respond, "Windows98(TM) is 17.7205875 sq. in.," which is approximately the surface area of a standard CD-ROM disk. The true measure of the size of Windows98(TM) is its information content, i.e., a certain number of megabytes. Properly speaking, then, we are asking how much information is contained in the fundamental units of physics, and how many smaller blocks of information must be cobbled together to produce that level of complexity.

    Nevertheless, there are ways to relate the scale of the automata to the scale of the phenomena with which we are familiar. One proposed "natural" unit of length is the Fermi, which is the range of the strong nuclear force. Another much smaller unit is the Planck length, which is derived from the three fundamental physical constants of gravity (G), the speed of light (c), and the quantum of action (h).

    In the final analysis, the scale does not impact on the features of the cellular automaton computer being investigated. Whatever the scale, we may think of the fundamental units of length, mass, time, and all other properties as "1", at which point the scale is immaterial. Without choosing among these possible "fundamental" units of length, Fredkin notes that the number of such units contained in the area occupied by, say, an electron (considering the size of an electron as its wavelength, and not as a point particle), is enormous. At any plausible scale, such a vast number of cells, considered as bits of data, would be sufficient to represent a huge amount of information.