A Quantum Dialog

The story you are about to read is true. The names of the phenomena have been changed to protect the rhetoric.

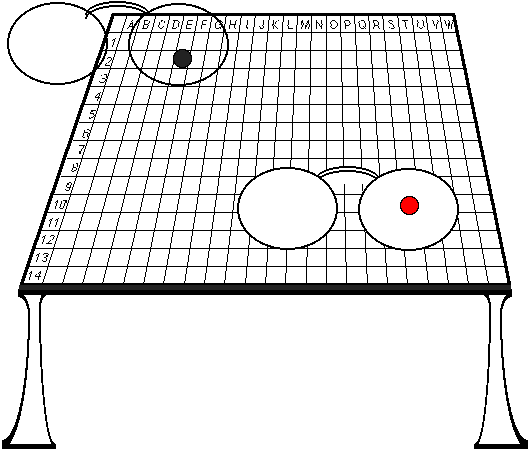
"I have a collection of red and green balls. When you are not looking, I am going to place them one at a time on a table with a grid. Then, I want you to tell me what is the color of the ball and where it sits on the grid."

"Okay."

"Now, you must make your observations using one of two pairs of glasses: The first pair of glasses makes you colorblind, so you cannot tell the difference between a red ball and a green ball; we'll call them the 'position-checking glasses'. The second pair of glasses hides the grid, so you cannot tell where the ball sits on the grid; we'll call them the 'color-checking glasses'."

"Okay."

"Now turn your back. Put on the color-checking glasses. Turn around, look at the ball through the glasses, and tell me what color is the ball."

"Okay. The ball is red."

"Good. Now check your observation."

"Okay. The ball is definitely red."

"Good. Now switch glasses and tell me again where the ball sits on the grid."

"Okay. The ball is sitting at grid coordinate E, 2."

"Good. Now check your observation."

"Okay. The ball is definitely sitting at grid coordinate E, 2."

"Now switch glasses again, and tell me again what color is the ball?"

"Hey, wait a minute. Now the ball is green."

"Are you sure?"

"Yes. It's definitely green. Did you switch the balls?"

"I did not switch the balls. Now switch glasses again and tell me where the ball sits on the grid."

"Hey, wait a minute. Now the ball is sitting at coordinate B, 1."

"Are you sure?"

"Yes. It's definitely sitting at B, 1. Did you move the ball?"

"I did not move the ball."

"Did you move the grid?"

"I did not move the grid. Now we're going to continue this game all day long."

[Sure enough, our friends continue the game all day long and well into the night. After tallying the day's results, they find the following:

1) that the ball is either red or green exactly 50% of the time on first observation, and that the ball is at some random point on the grid on first observation.

2) that a red ball stays a red ball (and a green ball stays a green ball) on each successive observation of color, so long as no observation of position is made. Similarly, position is constant so long as there are no intervening observations of color.

3) that whenever a color observation is made after a position observation, the color of the ball is either red or green exactly 50% of the time. Similarly, whenever a position observation is made after a color observation, the ball is found to be at a random position on the grid.]

"Fine. Now, what do you conclude?"

"Umm. I conclude that the ball is either green or red, and that when I look at it steadily it does not change; but that when I look away to check its position, it sometimes changes color and sometimes doesn't change color."

"That's a good start. Now, let me ask you some questions. When I first picked up the ball out of the pile of red and green balls, I had it hidden from you. You couldn't see it. At that time, what could you say about the ball's color?"

"Umm. I could say it was either green or red."

"That sounds reasonable. Now after you saw what color it was, what could you say about the ball's color?"

"Umm. I could say it looked green, or it looked red, depending on how it looked."

"Good. And if I never asked you for it's position, what could you say about the color of the ball?"

"Umm. It would continue to look the same color as it looked when I first checked its color."

"Good. Now when I asked you to check it's position, what could you say about the color of the ball?"

"Umm. I could say it was either green or red."

"Again, that sounds reasonable. Now, listen carefully. Suppose that when you first checked its color it was green, and then you checked its position. Did your knowledge that it was green the last time you checked its color help you in any way to know whether it would be green or red the next time you checked its color?"

"No."

"Good. What do you conclude?"

"Umm. Well, it seems like every time I check on what color the ball is after I check the position, everything starts from scratch as far as what color the ball is. It's like the ball didn't have any color until I checked it for color, and then the 'color' I see is just a randomly chosen color having nothing to do with the particular ball you took out of the bag."

"Very good."

"Are you sure you're not switching the balls?"

"I'm sure I'm not switching the balls. Now let's examine the ball's position. When I first put the ball down and you had your back turned, what could you say about the position of the ball?"

"Umm. I could say that it was on the table somewhere, within your arm's reach."

"That sounds reasonable. And after you had checked the color of the ball, what could you say about the ball's position?"

"Umm. I could say that it was on the table somewhere, within your arm's reach."

"Reasonable again. And did your knowledge of the position of the ball from your last observation help you in any way to know the ball's position when you next checked it after observing its color?

"No."

"Good. What do you conclude?"

"Umm. It's just like the color. As far as I know, the ball's initial position is random; and when I check the color of the ball, the position returns to a state of randomness."

"Very good."

"Are you sure you're not switching balls? Moving them around? Moving the grid?"

"I'm sure. I'll let you in on a little secret: they're not balls. They're just images of balls."

"Oh, you mean like holograms."

"Yes, like holograms. And they don't have any intrinsic color. When you put on the glasses to check for color, the glasses send a signal to the computer querying for a color; the computer dips into a completely random series of Rs and Gs, and returns either 'Red' or 'Green,' depending on whether it came up with a random R or a random G. The glasses you are wearing then supply the color that you see."

"Okay, that's plausible. What about the ball's position on the grid?"

"Same thing. The position-checking glasses call for a grid which is supplied by the computer and projected onto the glasses."

"Oh. How come the color value is displaced when I get a position value, and vice versa?"

"The two values use the same spot in memory, which can only hold one value at a time. It's fine as long as you keep checking only the color. The color value stays put in memory. But when you check for position, the color value is displaced by the position value, and must be calculated again the next time you check for color. Color and position are examples of what I call 'superposed' properties, because the calculations for each must be superimposed on the other. That's a little joke."

"Boy, these are really good glasses. The balls look so real."

"Thank you.
"Now I'm going to roll the ball along the table. Tell me what you see."

"Umm. I see the ball rolling along the table."

"Good. Now I'll stop the ball.
"Now here's another good pair of glasses that I have. They're magnifying glasses. Put them on and look at the ball. Tell me what you see."

"Oh, okay. Now I can see that the ball is just an image of a ball. "

"How can you tell?"

"With these magnifying glasses, I can see that the image is broken into pixels, discrete squares. They were so small I didn't notice them before. It looked like a smooth, continuous line."
"Good. Now I'm going to give you a good button that I have. It's a slow motion button. I'm going to roll the ball along the table again, and I want you to push the slow motion button. Here goes."

"Okay, now I can see that the ball is just a series of images of the ball."

"How can you tell?"

"When I push the slow motion button, I can see that the ball doesn't really roll along; it jumps from one position to the next position, and to the next, and so on. Now it's falling off the table, picking up speed, and the only difference is that it moves further from one jump to the next. Just like a movie, or my videotape player."

"Good. What do you conclude?"

"All day long, I've been watching a computer-generated movie of a ball when I thought I was watching a ball. Boy, that's a great computer."

"Thank you. You may now take off the glasses and put away the button."

"I don't want to take off the glasses. Tell me, friend . . .."

"Yes? What's the matter?"

"It's you. I'm looking at you now, through the magnifying glasses, and it looks like you're made up of little pixel squares, just like the image of the ball."

"That's absurd."

"It's true. And, wait a minute . . .. I'm going to push the slow-motion button. Hey, why are you moving in such a jerky way, just like the ball did?"

"I'm . . . su . . . re . . . I . . . don . . .'t . . . kno . . . w . . .wh . . . at . . . you . . .'re . . . tal . . . king . . . ab . . . ou . . . t."

"So. It's not just the ball you're a holographic movie projection, too!"

"That's absurd. How can you say that when we've been such good friends?"

"And the table . . . and the chairs . . . and the door . . . and the lightbulb . . . and look! My feet! They're pixels, too! Now I'm going out the door . . . Look! The front walkway! And the trees! And look at my hand! Pixels, all pixels!"

What do you conclude, Mario?

Great Neck, New York
April 28, 1997