No discussion of quantum mechanics would be complete without mention of a few more of the oddities of this underlying structure of our universe. I want to discuss three experimental results in particular, because they demonstrate in simple and powerful ways the nonphysical nature of our world. They highlight the truth of one of the fundamental axioms of quantum mechanics, which is that the mathematics are more "real" than the observations we make of any "particle" that appears to our senses.

The reality of numbers. The nonspecific quality of a quantum unit's location has other consequences for its behavior. I want to mention one of these behaviors because it is a particularly absurd result of the mathematical description of the quantum unit -- in this case, an electron. Absurd though it may be, it is quite "real" in the sense that it actually happens. This particular quantum "effect" gave somebody the idea to design an electrical circuit based on it, and the circuit works. It is called a "Josephson junction," after Brian Josephson, who first demonstrated the principle, and it is part of many of the electronic devices you use every day.

     The Josephson junction is a technique for regulating the flow of electricity. Now, if you were designing a circuit to limit the flow of electricity, you might use a very thin wire, or a wire made out of something that doesn't conduct electricity very well, or some other scheme for limiting the electric current according to "classical" electronic techniques. You probably would not think to place a barrier which does not conduct electricity at all -- at least, not if you wanted to get some electrons through. But the Josephson junction does just that. It places a complete barrier in front of the electrons, so they can't get through at all -- at least, not in the usual way.

     Let us consider an electron unit as if it were a little billiard ball, and put it inside a box. Ordinarily, it's just going to bounce around inside the box, right? If we want to get it outside the box, we would have to knock it very hard, and perhaps bust through the side of the box. But that would be very hard on the box, and we might not be able to use the box for our next electron.

     But, by now you should realize that electron units are not like little billiard balls, and their location property is a much more subtle quality than we can imagine if our model is a billiard ball. In fact, unless and until you measure it, the location property of an electron is quite literally a mathematical probability, rather than a spot. (Remember that this is how an electron unit can go through both slits of a double slit experiment to form an interference pattern at the detector -- unless you measure it's location at the slits, in which case it has a location at the slits, and then it's a billiard ball again because that's what you were looking for.) So let's not measure the location property of the electron unit inside this box. Let's close the box and not look inside. If we do that, where will the electron be? We put it inside the box, so it has to be inside the box, doesn't it? Well, not necessarily.

     Unless and until we measure the location of the electron unit, it's location is described mathematically by a probability curve -- a wave of probability. So, if we close up the box and stop looking, the actual state of the electron unit's location will be something like this:

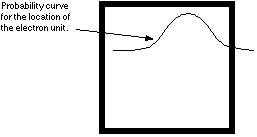
     So how are we going to find out? We will measure its location, of course. And when we do that, when we measure the location of the electron unit, it will have a location. And the actual location that will appear when we measure it will be in strict accordance with the probability curve we see above. And that means that it will usually be found inside the box. But that also means that, every once in a while, it will appear outside the box. This will occur randomly with respect to each individual measurement (that is, the location which will appear for any particular measurement will be completely unpredictable), but the overall result will reflect the precise mathematics of the probability curve.

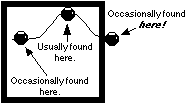
     Apart from being a neat trick, and a commercially valuable engineering design tool, the Josephson junction is a fine demonstration of one of the fundamental principles of quantum mechanics: the statistical model of probabilities is more real than any aspect of the quantum unit that we can measure, test, probe, touch, see, or otherwise observe. In quantum mechanics, the mathematics determines the behavior of the system, no matter how bizarre that behavior might seem to us. We must, finally, stop thinking of electrons and photons and such as "particles" or any other kind of substantive objects, and begin to accept that they are first, last and always mathematical objects which will always "behave" like formulas and algorithms; that is, they will always produce the results that a computer would produce if fed the formula or algorithm as its input, and the product of those calculations will constitute the "behavior" of the object.

Albert Einstein in the great scheme of things. The next two oddities I want to discuss have a common origin in the thoughts of one of the great thinkers of our century, Albert Einstein, and so this would be a good time to consider the man and his ideas. Einstein deserves the title "Great Thinker" more so than most, in part because that describes his theoretical methods more so than most. In 1905, this little known clerk in the Swiss Patent Office (with a solid education in physics from the Zurich Polytechnic Institute) produced a few short papers, which he submitted to scientific journals. One of these drew on only a few basic observations made by earlier physicists, and presented only a few equations (and fairly simple ones at that), and proceeded to lay out a concept that was absolutely breathtaking in its scope and originality. The concept was relativity and, as amplified by Einstein in 1916, it remains today as a cornerstone of modern science.

     Retrospective appreciations of Einstein's 1905 paper on "special" relativity have sometimes described it as the product of "pure thought."[2] That is, it seemed as though Einstein had considered certain paradoxes that had been puzzling physicists, had given the matter some thought, and had written down a new model of the universe. The principal "experiments" that he cited in supported of his conclusions were called "thought experiments," because he simply imagined various situations, applied the known behavior of physical systems, and came up with the result. The theory of relativity appeared to spring fully grown from Einstein's forehead, in the manner of a scientific Athena. In this regard, Einstein's methods actually hearkened back to the philosophical schools of Zeno and Democritus, using the human mind as a laboratory and logic as experimental apparatus. Just as Zeno did not need to observe how a moving system would behave in "quantized" or atomized time in order to deduce how such a system must behave, so Einstein did not need to travel at the speed of light to know how matter and energy must behave under such an extreme condition. In both cases, these philosophers, ancient and modern, were dealing with situations which could not be measured experimentally with the techniques of the day, and so the only way to experiment was with the mind. Pure thought.

     Einstein's name and reputation are so tightly bound to the theory of relativity that his other contributions to science are often forgotten. Einstein's Nobel Prize was awarded in 1921 for another of his little papers of 1905 -- a paper which solidified the quantum interpretation of the odd step-like behavior of light which had been noted by Planck in 1900. (In 1921, the theory of relativity was still considered suspect; quantum mechanics, no matter how bizarre, could be demonstrated in the laboratory.) Einstein dealt with Planck's observations of the peculiar fact that when you heat something, it gives off light only at certain "wavelengths," not at others. This odd quality of "blackbody radiation" led Planck to deduce that the material exchanged energy only in discrete units, rather than continuously. Planck's hypothesis was tentative, but it fit the experimental results. Einstein used Planck's idea of noncontinuous emission of radiation to explain another discontinuous phenomenon, the "photoelectric effect" which occurs when light shines onto metal, causing an electric current to flow. Einstein suggested that the light hitting the metal was itself particle-like, and he produced equations that would govern its behavior. Recall that the wave theory of light was well established at this time, despite the perverse results of the Michelson-Morley experiment. Being immersed in their wave tanks, physicists could not explain why some frequencies of waves would be allowable, and others not. It was as though a sunbather at the beach noticed that waves crashed every six seconds in the morning, every five seconds from noon to 2 o'clock, and every three seconds until dusk -- and that they never varied from this routine, and never crashed at any other or different intervals. This would not make sense to anyone who considered the ocean a vast continuum with as many different sizes of waves as there are grains of sand or stars in the sky or numbers in the universe. Einstein's analysis demonstrated how this effect could be achieved by a mathematical model of light consisting of Planck's "quanta." While this recalled the particle theory of light, Einstein did not exactly insist that light was made up of particles; rather, he showed that by thinking of "packets" or "quanta" of light, the results of the experiments could be explained neatly. Einstein thereby began the "dualistic" interpretation of light, whereby it was sometimes best compared to a wave, and sometimes to a particle -- a concept which became the basis for most of the quantum mechanical interpretations which followed. Einstein thereby took Max Planck's insight and put it on a secure mathematical foundation.[3]

     Einstein helped to lay much of the foundation for quantum mechanics in the same burst of intellectual wizardry that produced the theory of relativity. Einstein himself appreciated the irony of this situation, and he spent much of the remainder of his life trying to reconcile the two concepts which, when extended, seem to produce conflicting models of our world. For it was in the extension of quantum theory that Einstein parted company with quantum theorists such as Niels Bohr, and, in part, this was because these extensions of quantum theory seemed to conflict with his own more deeply held beliefs that gave rise to relativity.

Action at a distance. One of the fundamental principles that emerged from relativity was that nothing could exceed the speed of light. This was one of the handful of rock bottom assumptions which led Einstein to the theory of relativity -- a theory which has been as astoundingly successful in its own sphere as quantum mechanics has been in its sphere. Although the statement has been modified somewhat to accommodate various extensions of relativity itself, it is still held out as a universal law of physics. By Einstein's model, nothing happens instantaneously; all interactions require time, and the time cannot be less than it would take for light to travel between the two locations that are to interact. Einstein was among the first to realize that if quantum mechanics was correct, it implied that this law would be broken in some situations. This led to the first of a series of intellectual battles between Einstein and Bohr.

     In quantum mechanics, each "quantum" (electron or photon or otherwise) is described in terms of a mathematical function. These mathematical functions sometimes can merge, and can be "split," in the way that two passing wave crests can merge and split. In quantum theory, the merger of two quantum functions can be described completely by one combined function. This means that, when the merged quanta are later separated, they will always and forever continue to be just two parts of a single wave function.

     Einstein thought about this. He also thought about the uncertainty principle. And he realized that, in certain situations, the combination of the wave function description of matter and the uncertainty principle would lead to results which seemed to contradict his own principle that all "communication" is limited by the speed of light; that nothing can happen "simultaneously" when they are separated by distance -- any distance. And so Einstein, together with two colleagues, Boris Podolsky and Nathan Rosen, designed a "thought experiment" tactfully to point out this inconsistency to Bohr. This thought experiment is known as the "Einstein-Podolsky-Rosen Paradox," or just the "E-P-R Experiment" for short, for its three proponents.[4]

"Suppose," suggests Einstein, "that two quantum systems merge so that they can be completely described by a single mathematical function; and suppose that these two systems are then separated. The merger of the two systems implies that their quantum properties are identical at that point, because the mathematical function has room for only one number in each of the quantum categories. When separated, they will continue to have these properties in common."

"So far, so good," replies Bohr. "You mean that, for example, if two photons were brought together, they would have the same polarity -- because each photon has one and only one polarity; and if we then split this combined photon in two, say, with a beam-splitting mirror, they would each continue to have the polarity they had when combined. I agree."

"Good. Let us use your example of the photons. Now we know," continues Einstein, "that you cannot determine exactly what the polarity of a photon is until you measure it, right?"

"That's correct," answers Bohr. "In a sense, the photon doesn't have a polarity until you measure it."

"But," clarifies Einstein, "if and when you measure it, it will have a polarity, right?"

"Right," says Bohr.

"And if you measured one of these two photons which have been merged and then split, and the polarity turns out to be, say, 'vertical' (as opposed to 'horizontal'), then the other photon will also have to have a polarity of 'vertical.' Right?"

"That's correct," says Bohr. "Since the two quantum systems have been combined, they will exhibit the same quantum properties, including polarity."

"Okay," says Einstein. "First you say that you cannot, even in principle, determine what the polarity is before you measure it; then you say that once you have measured the first photon, you know that the second photon will have the same polarity."

"That's correct," answers Bohr. "That's what the math dictates."

"Now," says Einstein, with an air of triumph. "Suppose you split your photon into two photons; and you send them off in different directions; and then you measure your first photon. Your first photon didn't even know what it's own polarity was before you measured it. And yet, all of a sudden, your second photon does know what its polarity is, because it has to be the same polarity as the first photon!"

"Uhm, let me think," says Bohr, playing for time. "Well, yes, I guess that's correct."

"So tell me, Mr. Bohr," says Einstein smugly. "How does the second photon know about the results of your measurement of the first photon? Did it get a letter in the mail? Did it have a spy in the next room where you were measuring? How?"

"Well I don't know how," say Bohr evenly. "It just does. It does because the math says it does. Don't ask me how it knows, that's a meaningless question."

"Meaningless to you, perhaps. You admit, do you not," continues Einstein, pressing his advantage, "that this knowledge arrives at the second photon instantaneously, having nothing to do with the speed of light? And having nothing to do with how far they may be separated, yea, unto the ends of the universe?"

"Correct," says Bohr.

"So the information has somehow got from the first photon to the second photon faster than the speed of light."

"I guess you could put it that way," says Bohr.

"That is impossible," concludes Einstein.

"That is the way it is," concludes Bohr.

     When Einstein and Bohr and their colleagues were having this little discussion, it seemed entirely hypothetical. There was no way at the time to put the theory to the test. Nevertheless, Bohr stood firm in his conviction that this situation would result in exactly the type of instantaneous correlation of the quantum properties that Einstein envisioned. And Einstein stood firm in his conviction that such a thing was impossible. In 1982, the matter was finally put to the test in a convincing way which seemed to support Bohr's view, relying on a mathematical analysis of measurements developed by John S. Bell in the 1960s.[5] More recently, in 1994, the experiments were refined in a way which seems even more to support the quantum mechanical description of these systems. And so, Bohr is generally credited with having won the argument.

     Whether Einstein liked it or not -- and whether Bohr could explain it or not -- it appears that quantum mechanical systems do remain connected in their mathematics, and so in their properties, when separated by distances, no matter how vast. Einstein considered two separated particles to be two separate entities, which would have to talk to each other in some manner.

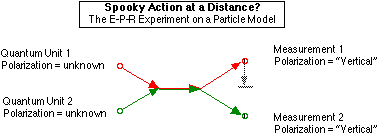
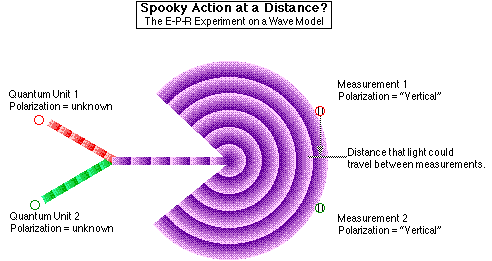
     Relativists take comfort in the fact that, despite this apparently instantaneous "communication" between the quantum units, there does not appear to be any way (even in principle) to generate any communication by this method which would be meaningful to an observer. Therefore, relativity's assertion that nothing can travel faster than light has simply been restricted to stating that no communication which would be meaningful to an observer can travel faster than light. This qualification was no comfort at all to Einstein. To Einstein, the universe should run by law and principle, not by magic; and no matter how the quantum theorists hemmed and hawed, it all seemed like magic to Einstein.[6]

Spreading probability waves. Einstein had further insights into the uncertainty principle which he reached by mathematical analysis. Recall our discussion of the relationship between position and momentum, as illustrated by the state trooper trying to give out a speeding ticket. (Chap. xx, pp. xx-xx.) The basic premise is that the more accurately you measure the momentum (i.e., the speed), the less you know about the position. In the example of the state trooper with his radar, we imagined that as the trooper increases the accuracy of the radar measurements he is taking, the car seems to spread out along the interstate.

     Einstein thought about this. He thought about what would happen as one pinpointed more and more precisely either the speed or the position of a quantum unit. What would be the physical result of such increasingly precise knowledge, according to quantum theory? Together with a colleague, the Indian physicist S. N. Bose, Einstein worked out a mathematical description of such a situation. Suppose, he suggested, one were to cool a few molecules more and more, so that they became colder and colder, and their momentum approached more and more nearly zero. What would be the consequences for the position of the molecules? According to Heisenberg, the increasingly precise knowledge of the quantum units' momentum would "cause" their locations to become less and less precise, regardless of whether you thought you knew exactly where they were, having pinpointed them earlier. If one were to observe such molecules in the process of cooling, what would you see? Einstein figured that the molecules must logically appear to spread out, just like the cars spreading out all over the interstate. Molecules near to each other would then begin to overlap, until, eventually, one would be left with a "soup" of overlapping particles occupying the same space. In physical terms, this concept became known as a "condensate," as though the molecular soup was "condensing" out of the cold like dew on the morning grass. Accordingly, this hypothetical agglomeration of smeared-out molecules became known as a "Bose-Einstein Condensate."

     Like the E-P-R thought experiment, the Bose-Einstein Condensate conjecture was purely hypothetical (or, rather, purely mathematical) at the time it was proposed. The temperature at which Bose and Einstein calculated the condensate would appear was only [a few billionths] of a degree above absolute zero, which was much too cold to achieve by any methods known at the time. However, the technicians became more and more clever at figuring ways to cool molecules. Beginning in the early 1980s, the effect began to be detected, and eventually, in [1996], the required temperature was achieved. And lo and behold, a condensate appeared -- many molecules smearing out into one big soup of a wave function. Once again, the math of quantum mechanics had triumphed.

Epilog on Einstein. After "losing" the debates with Bohr in the 1920s and 1930s, Einstein pretty well held his peace about his doubts on quantum mechanics. One colleague had gently chided him that he had been acting like the "classical" physicists who simply could not accept relativity, despite its demonstrable scientific effectiveness. Nevertheless, Einstein continued to feel in his gut that something was missing from quantum mechanics, no matter how well it seemed to work in predicting results. Bohr's insistence that there was nothing beneath the math, and that a property didn't exist in any meaningful sense until it was measured by an observer, was not a good enough explanation to Einstein. In fact, to Einstein, all of the precise description of quantum mechanics was no explanation at all.

    Einstein died in 1955, only three years after the debut of the world's first electronic computer, which used small punch cards to ask questions of the machine and produced more small punch cards to display the results of its calculations. This machine was thought to be very useful in eliminating the tedium of adding and subtracting, multiplying and dividing the numbers that physicists were constantly having to deal with -- in the same way that an automatic dishwasher was useful in eliminating some of the tedium of cleaning up after supper. Einstein never came up with a better explanation than Bohr's formulation of quantum mechanics.

1. [Back]	This characterization has been confirmed by an interesting experiment with light. As we shall see, one of the fundamental postulates of relativity theory is that nothing can travel faster than light -- not even light. Yet, when light is sent through the photon equivalent of a Josephson junction, it arrives at its destination slightly faster than a parallel beam that did not go through such a junction. Instead of slowing down the photon, the "barrier" speeds up the light. Why? Because the small distance represented by the barrier is missing from the path of the light. The light "jumps" past the barrier instantaneously, it does not go through it. The path with the barrier is shorter from the light's point of view, and, traveling at the same speed of light as the other beam, it will arrive at its destination sooner.
2. [Back]	C.P. Snow, Variety of Men, Penguin Books, Harmondsworth, U.K. 1969, pp 85-86.
3. [Back]	In a third little paper of 1905, Einstein dealt with the odd behavior of particles suspended in a liquid, called Brownian motion. It seemed that no matter how calm and still you made the liquid, these little suspended particles kept jumping and jerking around in apparently random motions. Einstein showed how this would be caused by the random motion of the molecules of the liquid itself, bumping into the suspended particles, and showed how the math worked. This analysis solidified the atomic theory that all "things" are made up of tiny little bits of matter, called atoms (and molecules). Before Einstein's analysis, the atomic theory had been more a conjecture than an established fact.
4. [Back]	The famous debates between Bohr and Einstein occurred between 1927 and 1930. The E-P-R thought experiment was presented by Einstein, Podolsky, and Rosen in 1935. A. Einstein, P. Podolsky, and N. Rosen, "Can quantum-mechanical description of physical reality be considered complete?" Phys. Rev., 47. The dialog presented here, however, is a purely imaginary dialectic.
5. [Back]	Alain Aspect, "Experimental realization of Einstein-Podolsky-Rosen-Bohm gedankenexperiment: A new violation of Bell's inequalities," Phys.Rev.Lett. vol. 49, nr.2, pp.91 (1982).
6. [Back]	See R. Penrose, The Emperor's New Mind, at 279-87, 286 ("Although EPR-type experiments do not, in the ordinary sense of sending messages, conflict with the causality of relativity, there is a definite conflict with the spirit of relativity in our picture of 'physical reality'" (emphasis in original).

The Reality Program by Ross Rhodes 9/15/02 The Notebook of Philosophy & Physics | Home Page | Essays |Links | Guestbook | Copyrights |