Fredkin begins his exploration of the universe with a simple observation: from the time Max Planck coined the terms "quantum" and "quantized," it has happened that every physical phenomenon susceptible of precise measurement has turned out to be "quantized." Einstein proposed in 1905 that light was so quantized that it was sometimes best thought of as "chunks" of energy, i.e., particles dubbed photons; Neils Bohr proposed in 19xx that electrons associated with an atomic nucleus were "quantized" in their ability to fill "shells" (see Chapter xx); the hypothetical intrinsic motion of quantum particles -- angular momentum or "spin" -- is an either-or quality with no in-between. We may go back further, to the theory of atoms which showed that everything -- earth, air, fire, water -- is comprised of discrete chunks of atoms and molecules as grainy as the sand, regardless of how smooth and continuous they might appear.

While other phenomena -- notably position and momentum, which is to say space and time -- remain undetermined, Fredkin reasoned that the clear tide of scientific progress seems to favor discreteness over continuity. As we discussed earlier (Chap. xx), what might seem continuous on the order of a motion picture might turn out on closer inspection to be a series of discontinuous events like frames of still pictures flashing by faster than we can count them. Fredkin speculated that it is most likely that all phenomena eventually will be found to be step-wise, discontinuous, quantized in their nature, rather than smooth and continuous. That is to say that nothing is continuous, despite appearances created by our limited powers of observation. Not light, not "fields," not space, not time.

Fredkin saw that a necessary corollary of all things being discrete and stepwise is that all things are thereby made finite. That is, there will be no infinity and no infinitessimal in our physics because those bothersome concepts occur only in the gaps between measurements, of which there are none if one discrete measurement abuts the next.

Fredkin called his thesis "Finite Nature," and he saw that this hypothesis, if true, poses the greatest challenge for physical theory. It is nothing less than Zeno's paradox in the flesh: if all things are discrete -- including most fundamentally space and time -- then nothing can change. There can be no evolution from the state that exists at one moment to the state that exists at the next moment because there is no transition, no morphing, no sliding, no movement, nothing in between. The thing exists at one moment, then it exists at the next moment. How, then, to account for the observed fact that the thing is different from one moment to the next?

The way to account for change is to see "properties" as finite sets of information. In dealing with a set of information, we see that it can change and transform only according to rules laid down by another set of information. This is the "process" of changing information, and it is the very definition of "information processing." It is also the very definition of a digital computer. Let us examine this two-part concept -- "digital" and "computer" -- according to Fredkin's analysis in Finite Nature.

Digital. The hypothesis that all things are discrete implies first that all things are finite. That is, there is no infinity and there is no infinitesimal. ("Whew!" says Zeno. "Whew!" says the quantum physicist.) No matter how big the numbers get, and no matter how small, there will be an end to them, and it will be a definite number. That's the difference between something that is infinite (or infinitesimal) and just really-really-big (or really-really-small). There is an end. It is definite. It is finite. Achilles will come to the point where there are no more half-ways, and so he will cross to the finish line. The quantum physicist will reach the end of the calculation, with nothing between him and zero.

A property or quality which is discrete and finite can be described exactly. For example, if a coin has the discrete and finite property of being heads or tails, then it cannot be anything in between.[2] Accordingly, when we observe that a coin is "heads," we describe the coin's state of-flip exactly.

Where the possible states are so limited, there is an exactly limited amount of description that can be given before we run out of things to describe, and ways to describe them. The state-of-flip (heads or tails, or simply "h" or "t") may be one property; and the place-of-minting (Philadelphia, Denver or San Francisco, or simply "P," "D" or "S") another; and the denomination (nickel, dime, quarter, etc.) may be another; and so on. Each of these properties, being limited to a certain number of possibilities, can be described with a single choice from among its finite possibilities.[3] We can see that with these restrictions, each coin can be described exactly by stating the value of each property of the coin.

Given Finite Nature, there are no approximations, no subjective values. A collection of three coins, in our example, can be arranged and rearranged in only so many ways before one runs out of possible combinations. Flipping one or another will yield different state-of-flip arrangements with exactly 8 possibilities, no more and no fewer:[4]

hhh, hht

hth, htt

thh, tht

tth, ttt

What is more, a property or quality which is discrete and finite, and which therefore can be described exactly, can be described exactly by a number. How fast? Sixty-three m.p.h. (as opposed to the alternative non-finite description, "rapidly"). The data itself, and thus the number itself, is the relevant information. In our coin example, heads could be represented by "0" and tails by "1", so that heads-heads-tails (or hht) could be represented by "0-0-1" or just "001." There is no difference in the information content between "heads-heads-tails" and "hht" and "001." What is more, there is no difference in the information content between the statement "three coins are lying on a table; two coins are heads up and one coin is tails up," and the symbolic number "001." So long as this property is discrete and finite, the number is all we need for a complete and exact description.

The interpretation of these numbers is easily accomplished simply by keeping track of what each digit is supposed to represent. In the previous example, the numbers represented a coin's state of flip. We could as easily have a secret code: if I say "one," you will know that I mean "by land"; if I say "two," you will know that I mean "by sea." Thus, by saying "one," I convey to you the entire sense that the-British-invasion-force-has-been-spotted-and-it-is-traveling-overland-to-attack-our militia-positions. And you have your further instructions that I intend by this signal for you to ride off on your horse to alert our militia forces to the nature of the threat. Because the interpretation of the numbers is necessarily arbitrary,[6] we will leave aside the question of interpretation for the moment to focus on the numbers themselves.

This is digital: numbers, digits. Information expressible as numbers. Digital information is a wonderful thing.

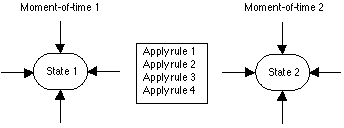
Computer. Now that we have all of these numbers exactly describing every property of every thing in existence, what shall we do with them? We can print them out in a very large spreadsheet, or as a very long string of numbers. That will give us a complete description of the universe at one instant -- every last pixel of one frame of the motion picture -- but it will hardly do as an arena in which to live out our lives. How do we get to the next frame, preferably without starting from scratch? From one moment to the next -- from one time-step to the next -- the information must be transformed completely to a new and different, but equally finite, set of information describing every property of every thing in existence as it exists at that next time-step.

We have one complete set of information, and the next complete set of information should bear some relationship to what we have. Therefore, we would like to change the present set of information into a new set of information that is somehow related. To do so, we will need a separate body of information consisting of rules for how this change should take place.

Put in terms of numbers, we have one complete set of numbers, and the next complete set of numbers should bear some relationship to the numbers we have. Fortunately, this is quite easy to do with numbers. We simply refer to a rule, or formula, or algorithm, or equation, by which we can transform one number into another. Here's a simple rule: multiply each number by two. The next set of numbers, according to this rule, will each be double the value of the previous number. If we perform this operation on each number in our spreadsheet, we will have a new spreadsheet with new numbers (each of which is twice the value of the corresponding number of the old spreadsheet), representing the next frame in the progression of our movie.

Taking one set of information represented by numbers, applying one or more rules for changing the numbers, and thereby obtaining a new set of information represented by a new set of numbers, is the process we call computing. For obvious reasons, it is also called information processing -- applying a process of transformation to a set of information. The information is represented by the numbers, stored in the computer; and the process of transformation is supplied by the rule or rules, stored elsewhere in the computer (also as numbers).

The clock -- a computer's quantized time. The computer's information is represented symbolically by the arrangement of binary switches in the computer's memory. The "state" of the computer is the aggregate arrangement of these memory bits. Consequently, when we consider the state of the computer, we must look at the arrangement in static, fixed form as it exists in its initial state and at the end of a step of programming. The arrangement cannot be changing as we consider it, because the "meaning" represented by the state of the computer depends on the relationship of each bit to every other bit.

The computer considers the information coded in its "state" and applies its programming rules to that information, changing the arrangement of the memory bits according to the rules. As the memory bits are being changed, the internal arrangement of the computer is in a state of transition. If the process were stopped in the middle of this transitional phase (before all of the rules for this "step" were fully carried out), an observer looking at the arrangement would not be able to extract any meaning at all. The overall arrangement would be "wrong" because the application of the rules had not been completed. This would be a computer crash.

To illustrate, suppose the memory bits were soldiers lined up in a row, and the rule was "take one step forward; then take another step forward; then take one step back." In our computer analogy, the sergeant must give these orders, one at a time, to each individual soldier, and each soldier then must carry out the orders. If we halted the process mid-application, we might see a very ragged line of soldiers because some had taken two steps forward and one step back, some had only taken two steps forward, and some had not yet moved. On the other hand, if we allowed the rule to be applied fully, we would see a tidy row of soldiers which had neatly advanced one step. If you had closed your eyes before the sergeant started (very quietly) giving orders, and opened them after he was finished, you might imagine that all of the soldiers had advanced one step all together. You would be wrong, but the net effect would be the same.

A computer achieves this tidy progression through a hardware technique called single clock. As Fredkin explains, "Single clock means that when the computer is in a state, a single clock pulse initiates the transition to the next state. After the clock pulse happens, various changes propagate through the computer until things settle down again. Just after each clock pulse the machine lives for a short time in the messy real world of electrical transients and noise. At the points in time just before each clock pulse the computer corresponds exactly to the workings of a theoretical automaton or Finite State Machine."

The single clock synchronizes the information processing in a computer, so that the programming can be applied in steps. At the tick of the computer's "clock," the programming is applied and the arrangement of the memory bits begins to change. After all memory bits have been affected, the clock tick is finished and the programming rule has been fully applied.

Edward Fredkin was in a unique position to discover the Rosetta Stone that would connect the seemingly disparate languages of physics and computer science. The link turned out to be cellular automata -- a method of programming computers according to a small number of simple rules which, when run repeatedly over a large number of cycles, developed the same dense complexity we observe in the physical systems of the natural world. Cellular automata programs have been developed to mimic the behavior of gas volumes, electrons traveling down a copper wire, ant colonies, and most famously the course of biological evolution in the "Game of Life." Fredkin saw applications of the cellular automata computer architecture everywhere he looked in physics. He began to believe that the match couldn't be a mere coincidence, and he formed the idea which has come to be known as the "Fredkin Hypothesis": the universe is a computer programmed according to cellular automata principles. More precisely, the universe is the manifestation of the calculations of a computer programmed according to cellular automata principles.

The Cellular Automata computer architecture. The cellular automata computer type of architecture provides a full analogy for the concept of discrete blocks of space-time which evolve, both individually and collectively, from moment to moment. This architecture denominates each computing unit as a "cell," which operates as though it were an independent computer with a simple set of programming instructions (although it is more accurately one of a large number of identical subroutines). Because the cell is operating independently and automatically, in robot-like fashion according to its rules, the cell is known as an "automaton" as though it were a robot performing its tasks mindlessly. The aggregation of many of these computing cells comprises the "Cellular Automata" computer architecture.

There is no difference in principle between the individual cellular automaton and any other computer. Both consist of a block of memory which is acted upon by a set of programming instructions. The difference in practical terms is that the cellular automaton operates according to a severely restricted set of instructions (programming), and so requires a comparatively modest amount of memory. With these limitations, we can create a vast number of cellular automata using our finite memory and programming resources. The key to the utility of the cellular automata ("CA") computer architecture is that when we assemble this vast number of simple, independent computing units, they can interact among themselves in breathtakingly complicated ways.

To illustrate, let us consider two simple cellular automata, side by side, whose only function in life is to have a color -- either blue or green or red. Each cell has only one rule to follow: it should ponder the color of the automaton next to it, and take the color which is next in line alphabetically. Thus, if its neighbor is green, it should take the color red; if red, it should take the color blue; if blue, it should take the color green. We can then watch as the situation changes over time (having arbitrarily assigned the colors Blue and Green to the automata to begin with):

Time step	Cell #1   Cell #2	Application of the rule
1:		Blue's neighbor is green, so it will become red; green's neighbor is blue, so it will become (remain) green.
2:		Red's neighbor is green, so it will become (remain) red; green's neighbor is red, so it will become blue.
3:		etc.
4:		etc.
5:		etc.
6:		etc.

. . . and so on. We have a pattern which, in this case, will repeat itself every six steps. Exactly the same rule is applied at each time step, but the pattern is slightly complex.

It is the interaction among the cellular automata which causes their states to evolve, and to evolve in a way that bears a relationship between past, present and future such that a pattern emerges.

Cellular Automata theory considers each automaton as a "cell" surrounded by other cells. Each cell acts independently in the sense that it follows its own rule or rules when deciding what it shall become in the next instant of time (just as in our simple example above). The rule of each cell is exactly the same as that of every other cell, and each takes into account the state of each of its neighbors and determines its next future state on the basis of the input received from its neighbors' present state, according to the rule.

Fredkin's conclusion that the particular kind of computer we have at the bottom is a cellular automata computer requires some additional understandings not fully discussed in his early papers. Nevertheless, we can see how the thesis that all things are finite introduces a compelling logic. Accepting Zeno's proof that a physical finite system cannot evolve, the premise leads to the conclusion that all things are computer:

As of this writing, Fredkin's ideas continue to meet with resistance from the moment he states his premise -- the very concept striking some as on par with alien abductions or some other cultic doctrine. Nevertheless, as physics moves closer to a paradigm of information, and farther from the mental image of specks and particles, there is some interest in what might be the implications of a universe operating on principles of information exchange.

In his book The Bit and the Pendulum, science writer Tom Siegfried surveys contemporary scientific thought from a number of fields and observes that scientists increasingly are resorting to information theory and the metaphor of information processing (computing) to explain a wide variety of problems in their fields. He includes an obligatory reference to Edward Fredkin's view, assessing it as follows:

In a column I wrote in 1993, I suggested that the chances that [Fredkin] is right are about the same as the chances that the Buffalo Bills will ever win the Super Bowl. So far, so good. The Bills have never won [as of 2000]. But they have made some of the games interesting.[9]

1 [Back]	Fredkin, Edward. "Finite Nature." Proceedings of the XXVIIth Rencontre de Moriond. 1992. -- "A New Cosmogony." Proceedings of the Physics of Computation Workshop. October 2-4, 1992. -- "Digital Mechanics: An Informational Process Based on Reversible Universal CA." Physica D 45 (1990), at pp. 254-70.
2 [Back]	The difference between these finite coins and the change in your pocket is that the coins in our illustration cannot be rolling, or on edge, of anything other than heads or tails. That is what we mean by a discrete, finite property.
3 [Back]	In this scheme, even such seemingly continuous properties as the general condition of the coin are limited to a set of choices -- such as "proof," "mint," "uncirculated," and "circulated" -- rather than being described along a full and infinite range of wear-and-tear. Although this type of limitation goes against common sense, it is required by Finite Nature and, in fact, it is a good illustration of the baffling step-wise behaviors of quantum mechanics.
4 [Back]	The reader can see why this limitation applies only to discrete properties. If we were to allow intermediate states such as the coin standing on its edge, and all of the instantaneous positions through which it can pass while rotating as it is being flipped, then there would be an infinite number of possibilities for the coin's state-of-flip property. The difference between eight possible states and an infinite number of possible states is our hypothesis that the coin can only exist in a complete state of being "heads," or alternatively in a complete state of being "tails," but never in between. Oddly, the scientific proofs that natural phenomena are fundamentally discrete rely on just this type of puzzling limitation.
5 [Back]	The possibilities would be the cube of 2 (three coins with two possibilities for each coin) times the cube of 3 (three coins with three possibilities for each coin), i.e., 23 x 33 = (2 x 2 x 2) x (3 x 3 x 3) = 216 possibilities.
6 [Back]	The meaning is anything the programmer wants it to be. As David Eck puts it, "Suppose I were to point to some particular sequence of bits inside a computer and ask what it represents. Without further information, the answer could be almost anything--the current date, the color of some particular pixel on the screen, the board position in a game of computer chess, Joe DiMaggio's batting average in 1939 .. .. What it actually means is determined not just by the sequence of bits but also by the physical structure of the computer itself, by the overall structure of the data encoded in the computer, by the program that is running, and by the intentions of the person using the computer." D. Eck, The Most Complex Machine, at 11(A.K. Peters, Ltd., Wellesley, MA 1995).
7 [Back]	G. H. Whitrow, The Natural Philosophy of Time, Clarendon Press, Oxford (2nd ed.) 1980.
8 [Back]	In his paper "Finite Nature," Fredkin does not address the ramifications of the E-P-R effect, whereby a quantum unit can be "influenced" by other quantum units far removed from its immediate neighborhood. However, other aspects of computer architecture may provide the most plausible explanation for this phenomenon. See R. Rhodes, "A Cybernetic Interpretation of Quantum Mechanics" at 13 (1999).
9 [Back]	Siegfried, Tom, The Bit and the Pendulum (John Wiley & Sons, New York, 2000) at 58.

The Reality Program by Ross Rhodes 9/15/02 The Notebook of Philosophy & Physics | Home Page | Essays |Links | Guestbook | Copyrights |