Chapter One

Ordinary Waves and Ordinary Particles

Waves are motion within a medium. Let us begin with the medium, and a few illustrations should suffice. For an ocean wave, the medium is the ocean (water). For a domino wave, the medium is dominoes. For a sports stadium wave, the medium is sports fans. For a sound wave, the medium is the air. In each of these instances, the "wave" is an overall impression, usually viewed from a distance, of movement within the medium. I say that the wave is an "overall impression" of movement because, although there is, in fact, movement within the medium, the actual movement is not what we generally think of as the wave itself. We think of the wave itself as the crests and troughs which move smoothly away from wherever the wave started. But the actual motion within the medium itself is more subtle, as we shall see.

Waves radiate. A simple water wave is generated by disturbing, i.e., moving, a body of water (the medium) at a point. This is often accompanied by a splash. The "wave" then appears to travel outward, away from the source of the disturbance. For a point source disturbance, such as a pebble falling into a pond, the wave radiates outward in an expanding circle, like so:

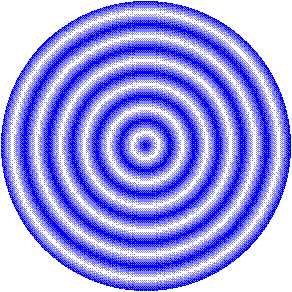
So long as the medium is widespread and surrounding, like water or air, the wave will radiate in these concentric circles.

Particles within the medium move, but only a little bit. If we think of the water as a great collection of particles, i.e., water molecules, sloshing around semi-independently, then we can examine the movement that takes place in a wave from their point of view. As it turns out, each "particle" of water exhibits only a limited kind of motion.

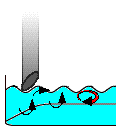
The falling object pushes down on the surface of the water, temporarily pushing the nearby water molecules outward and away from it.

When the object passes, these same displaced water molecules slide back into the "hole in the water" left by the object.

Each water molecule pushes on its neighbors in the same way that the falling object originally pushed on it. This carries the motion outward to the next, and then to the next, and on to the next water molecule.

The result of all of this pushing and sliding back is the appearance of a coordinated motion in the medium, which we see as a wave. In fact, each little water molecule is just going around in a circle.

    Let us consider the domino wave. This type of wave takes some preparation, in that we must stand a series of dominoes near each other in a line to create the medium. If we are careful, we can start a wave that will run all around the room:

With the domino wave, we have (1) the initial force (the flick of a finger) which starts the motion -- but having completed its push, it remains attached to the culprit and ceases to be any part of the wave; (2) the dominoes which fall one against the next -- but having bumped into the next domino, these remain approximately in their original position; and (3) the "wave motion," which is the passage of the force of the first domino's fall, transmitted through the medium (more dominoes) by one domino bumping into the next.

    How about the stadium wave? We have a wave traveling through the medium of sports fans, whereby each vertical row of fans successively stands, throws their arms up, and sits down.

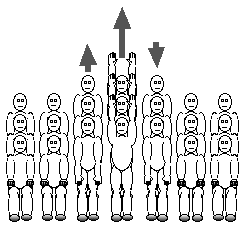
The "wave motion" is relative to the medium, not to the environment. We have been considering waves in essentially fixed media. That is, the water in our wave tank is still; the dominoes are still (until little brother comes into the room); the fans in the stadium are seated. If, instead, the medium itself is moving, then the wave motion will be affected. This is difficult to illustrate with dominoes or sports fans. However, you can easily imagine that, if you stand by a running stream and drop a pebble into it, the wave will appear to move upstream very slowly, but downstream very quickly. This is because the medium (the stream) is in motion, and it is the small motions of the particles, which are themselves in motion within this moving medium, that create the wave effect.

    The reason for this becomes clear if you look at the illustration of the particle motion in the wave tank: since each particle itself is in motion relative to the falling object, its displacement will be affected by its own motion; if it is already heading downstream when it is displaced further downstream, it will not bump very hard against its neighbor; on the other hand, if it is displaced upstream by the falling object, it will meet its neighbor head on.

    For your first exercise in relativity, imagine that you are in a canoe, lazily drifting downstream on a calm, flat stretch of river. If you gaze over the side of the canoe and look only at the water, you might think you were standing still; but when you look up, you see that the riverbank has been moving by. (From everybody else's point of view, the riverbank was standing still and you were moving by, carried by the river; but to you, it is as if the riverbank were moving past you. Welcome to relativity.) If you now take a pebble and drop it into the apparently still water beside the canoe, the ripples seem to form a familiar circular pattern, as though the medium (the river) were, in fact, still. From your point of view, there is no difference between floating along with the medium and being in a calm and still wave tank. However, to the observer on the riverbank, the medium (and you and your canoe) is obviously in motion, and so the ripples from your pebble seem to travel upstream only very slowly, but to speed along downstream.

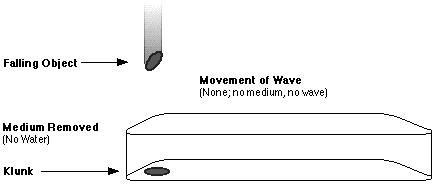
The wave needs its medium. To make a final point about the relationship of the wave to the medium, let us imagine what happens when one removes the medium. Suppose we drain the water from our wave tank. What will be the result?

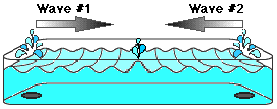
Overlapping waves affect one another by interference. Two or more waves passing in the same medium simply add or subtract their individual patterns in a straightforward manner. Thus, when two equal wave crests meet, they double their height.

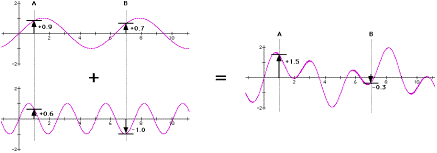
    By the way, computers are very good at this. The graphs in the illustration are simple sine waves. I produced the top wave by asking my calculating program for a graph of the function y = sin(x); the bottom wave is y = sin(2.5x); the combined wave is simply y = sin(x) + sin(2.5x). No problem. Which brings us to an interesting sidelight on how "waves" can travel.

Sound consists of waves in an air medium. The sound that we sense with our ears is a disturbance in the air around us. Because air is a medium which can be compressed, the disturbance travels as waves of compressed air (shock waves) radiating from the source. Using the example of a conventional loudspeaker, we can diagram the journey of a sound wave as follows:

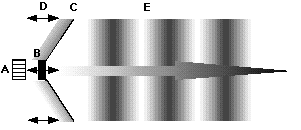
The sound wave itself is generated by anything from a tuning fork to a symphony orchestra. The tuning fork's sound wave is the simplest, being essentially a pure and regular sine wave, such as we have seen. The orchestra's sound wave is far more complex-looking, but it is essentially a simple combination of the many different waves coming from the various instruments, all of which combine by interference to form a final wave. Each individual instrument's wave is completely retained as one of the complexities of the final wave. Let us take an intermediate example of combining two tuning fork sound waves, which happen to be the sin(x) and sin(2.5x) with which we are familiar.

    In old-style recordings (such as a phonograph record), the resulting combination of these two waves is represented literally, as a wavy line scratched into the vinyl surface of the spinning disk. The groove representing the combination of our two sine waves, as above, would look exactly like the graph of the combined wave. A needle follows the groove and is pushed and pulled, back and forth; these needle motions are converted into electrical impulses with the same characteristics, which are fed to the magnet of the loudspeaker; the magnet then pushes and pulls the cone to produce the same wave pattern in a different medium: the air.

In modern digital recordings (such as a compact disc), this process is interrupted by an intervening translation of the wavy pattern into a string of numbers. The numbers of a CD recording are produced in exactly the same way that we calculated the combination of two waves earlier. That is, a computer measures the height or depth of the incoming sound wave at regular intervals, and records the resulting number as plus or minus.

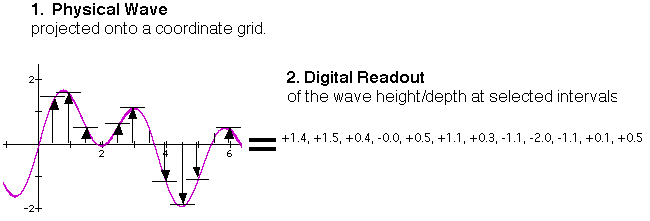
At any time we like, we can re-convert the string of numbers back into a graph by plotting the numbers, in which case we can use the re-created graphic wave to control the loudspeaker just as in old-style recordings; or, we can use the numbers directly to control the flow of electricity to the loudspeaker's magnet, and so to control the loudspeaker cone.

When symmetrical wave patterns overlap, they create a simple, symmetrical interference pattern. To return to our primer on the general characteristics of waves as experienced in our day-to-day, ground level existence, let us examine some very simple interference patterns.

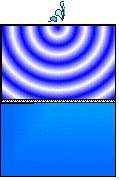
    We can create a nice effect by taking one wave pattern and superimposing it on itself. The combined wave pattern shows the cumulative effect of all the positive and negative reinforcing where the wave crests and troughs meet. Where the radiating wave patterns are identical, and only offset a little bit from each other, the result is a pleasing symmetrical interference pattern that appears as spokes going outward.
+ =

Waves passing through a barrier reproduce themselves. The behavior of waves passing through a slot in a barrier will become particularly important when we consider the first series of quantum mechanical experiments in the next section of this book. Fortunately, we have already been through most of the important points that we will need to bear in mind. But let us now take a look at this specific situation, using what we know about waves.

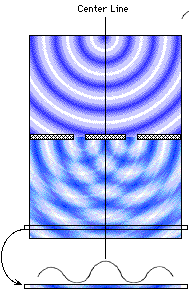
Using a wave tank, let us place a barrier half-way along the tank. The barrier will act like a breakwater in a harbor, stopping the waves coming at it (and reflecting them back toward the source). The water behind the barrier will be calm, cut off from the wave action.

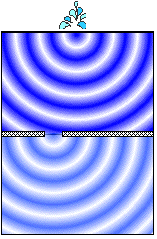
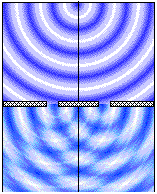
    If we take a cross-section of the resulting composite wave behind the barrier, we can see that it is as if we had cut through a bicycle wheel. We can count the spokes. Let us now "count," i.e., quantify, the wave as it appears in cross-section. We will graph the height of the wave along the cross-section, using the relative blue-ness (or darkness) of the pixels in the cross-section as our measure of wave height.

    Waves have many other interesting properties, but these are these are the properties I like to highlight, so that we can keep them in mind when we consider the results of quantum mechanical experiments. We will now consider the properties of particles as we experience them in our day-to-day, ground level existence. Fortunately, particles are a much more accessible and obvious quantity.

    Our main interest is in how a particle moves from point A to point B. Basically, the process is this:

the particle begins at rest, standing still;
we push the particle and it moves in the direction it is pushed;
if the particle runs into something that slows it down, it slows down until it stops; or
if the particle meets absolutely nothing to slow it down, it keeps going in the direction of the push forever at the same speed.

    Particle motion is much easier to think about than wave motion. With particles, what you see is what you get. The particle starts at point A; we push it toward point B; it moves toward point B; and if all goes well, it arrives at point B. We can measure the particle at point A (i.e., we can weigh it, note its color and shape, etc.). We can track the particle on its journey. We can measure the particle again at point B. Unless we did something to the particle in the meantime, it will be the same particle at point B as it was at point A.

    Here are a few more statements about a particle's motion, all of them fairly obvious:

when the particle leaves point A, it is no longer at point A;
while the particle is in transit between point A and point B, it is not at point A and it is not at point B, but is at some point between A and B;
when the particle arrives at point B, it is not at point A;
it takes time for the particle to move from point A to point B, and the amount of time will depend on its speed, which in turn will depend on how hard we pushed it.

    Of course, there are many situations in which a particle does not move in a straight line forever. Consider the path of a billiard ball which has been given a push by the cue stick. It begins slowing down immediately because of friction with the felt that covers the top of the pool table. It will change direction sharply when it hits a side bumper and rebounds. It may bump into another billiard ball on the table and bounce off in a different direction; or it may be struck by another moving billiard ball, and so have its direction changed. If pushed by a skilled billiards player's cue stick, it may even curve -- because the original push was given in a way that put a spin on the ball, and the spin causes the ball to move sideways at the same time it is moving forward. In all of these situations, we have another force acting on the billiard ball to slow it down or change its direction. If we did not have any such force, the ball would roll straight and true.

With these behaviors in mind, we may compare and contrast particle motion with wave motion.

Particles do not radiate. If we consider just a single particle, it will travel in only one direction at a time. (Of course, we could scatter a group of particles in such a way that they would fly off in all directions. But each particle of the group would go off on its own in only one direction at a time.)

Particles move by the entirety from point to point. The particle may be thought of as a single point, which will stay a single point at all times. The motion of the particle is just that -- one particle moving from point A to point B.

When particles run into each other, they just bounce off. Particles do not combine or otherwise modify each other by interference. Although we could certainly imagine two particles of clay hitting each other and "combining" to form one larger lump of clay, this is not what we think of as particle behavior; and, in any event, this type of lumping is in no way comparable to the complex interactions of overlapping waves which produce patterns over an expanding, radiating area.

Particles passing through slits in a barrier just go right through, and continue on a straight line (until something gets in their way). There is nothing complicated about a particle heading for a barrier with a hole. Either the particle will hit the barrier and be stopped (or bounced back), or it will go through the hole and keep going. (We will not worry about the particle hitting the side of the hole and being deflected as it goes through, although, of course, this would also be possible with a particle.) Using billiard balls as our model, we may diagram the possibilities as follows:

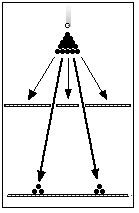
    Recall that, when we measured (or quantified) the wave interference pattern along the back wall, we found that it described a curve according to the relative height or depth of the wave crests and troughs along the cross-section. With particles, we will not find any similar curve, because each billiard ball moves independently from point A (the rack which is the starting point) to point B (the back wall). These billiard balls each hit the back wall one at a time, with the full force of one entire billiard ball, along their straight-line paths. That is how particles behave in our day-to-day, ground level experience.

    I suppose that particles have other interesting properties, but these are the properties I like to highlight, so that we can keep them in mind when we consider the results of quantum mechanical experiments. In the next chapter, we will look at a series of experiments conducted with quantum units such as photons, electrons and even whole atoms. As we progress in these experiments, we can put ourselves in the position of the person conducting the experiments by first deciding what we would expect to happen in the experiment, based on what we know about how things work in our experience; then taking a hard look at what actually happened in the experiments; and finally joining a long and distinguished line of great thinkers in trying to puzzle out what it all means.

The Reality Program by Ross Rhodes The Notebook of Philosophy & Physics | Home Page | Essays |Links | Guestbook | Copyrights |