Chapter Two
The Double Slit Experiments
We begin with light
The original double slit experiment (1802)
The Michelson-Morley Experiment (1881-87)
Double slit experiment with electrons
Re-examining the original double slit experiment using
particles
Trying to examine the process
The difference is knowledge
The measurement effect
Tell me something I can use in the real world, like my
kitchen
We begin with light.
What is the nature of light? This question has been posed in many forms for
thousands of years, with varying answers. In the late 1600s, Sir Isaac Newton
came out in favor of a particle view of light, and he called these particles
"corpuscles," which is simply another word for particles. Newton's
monumental work on the mathematical principles of science (or "natural
philosophy" as it then was called) was published in 1687. Newton never went
on record as stating that light had to consist of particles as a law of nature;
but he did state that this seemed to him more likely than light as a wave
phenomenon.
At around the same time, the Dutch scientist Christiaan Huygens was arguing that light consisted of waves, which was a view also held by an English contemporary of Newton's, Robert Hooke. By 1800, Newton's views were widely (but not universally) accepted. For one thing, Newton's other descriptions of nature seemed to work so well that scientists were inclined to give him the benefit of the doubt. For another thing, scientists were able to observe that light seemed to travel in straight lines for the most part, and this behavior was most easily explained by reference to particle motion.
The original double slit experiment. In 1802,
the British scientist Thomas Young hit upon a way to test the nature of light,
using a double slit apparatus. He reasoned that if light consisted of particles,
it would travel in straight lines from a source, through two slits in a barrier,
and on to a screen placed at the back of the apparatus; at the screen, it would
appear as two stripes of light. On the other hand, if light consisted of waves,
it would radiate outward from the source toward the two slits, pass through the
two slits, and begin radiating anew from each of the two slits as it traveled
toward the back screen; at the screen, it would appear as a series of stripes of
light, representing the interference pattern typical of overlapping, symmetrical
waves both emanating from a "stripe" in the barrier, i.e., one of the
slits. The two possibilities can be diagramed as follows, and these should be
reasonably clear from the review of particle and wave properties in the previous
chapter:
The Michelson-Morley experiment, pointing to a fundamental problem concerning these light waves. Now, as we have seen in the previous chapter, calling something a wave carries with it certain baggage. Among the most basic requirements recognized by scientists was this: if there is a wave, there must be a medium. This is the very nature and essence of a wave. Without a medium, there can be no wave. We don't care what the medium is -- air or water or dominoes or sports fans will do -- but a medium there must be. It had already been firmly established that light can and does travel through a vacuum with complete ease; and a vacuum, by definition, is a space where we have removed absolutely everything that is capable of being removed. Therefore, it appeared that the medium through which light traveled was something so all-pervasive that it filled even a "vacuum."
And so, with unassailable logic, the scientific community theorized that the entire universe was filled with a medium through which light waves traveled. This hypothetical medium was called "æther," from an ancient Greek concept of a rarefied substance thought to fill the upper reaches of the heavens. The aether was considered "hypothetical" only in the sense that it had not been detected directly; but, given the fact that the waves themselves had been detected directly (or so it was believed) in Young's double slit experiment, there was no other conclusion but that the waves were traveling through a medium of some kind. "Æther," then, was just a shorthand way of saying "the medium in which light waves travel" -- whatever that might turn out to be.
In 1881, the American scientist Albert Michelson invented a device so exquisitely sensitive that it was thought to be capable of detecting the aether. His invention, called an interferometer, drew on two of the wave properties that we reviewed in the previous chapter. First, there is the phenomenon of wave interference itself, which had been so convincingly demonstrated by Young's experiment. That is, when two symmetrical waves are offset -- even by the tiniest little bit -- they immediately produce a distinct and instantly recognizable interference pattern. Hence the name "interferometer," meaning a device (a meter) which measures wave interference.
The second wave property drawn on by Michelson was the behavior and appearance of a wave in a medium which itself is in motion. If you recall from the previous chapter, a wave will appear to travel "upstream" more slowly, and "downstream" more quickly, when the medium itself is in motion, such as in a flowing river. That is the way it looks to the observer standing on the riverbank, even though the wave is perfectly symmetrical when measured against the moving river itself. Michelson's logic was as follows:
If the aether pervades the entire universe, then anything that moves will be in motion relative to the aether. That is to say, we can think of the aether as a large ocean of a medium; we can then think of everything in the universe as being like a fish or a buoy or a scrap of algae -- floating or moving through the ocean of aether.
This being the case, we know that the earth is moving. It spins on its axis once every 24 hours, so that the earth's surface is moving at about 1,000 m.p.h. at the equator. The earth also revolves around the sun at about 65,000 m.p.h. Even if, by some fantastic coincidence, one part of the earth happened to be exactly still with respect to the aether at some point in time, in 12 hours that same location would be traveling at up to 1,000 m.p.h. in the opposite direction, and so would be in motion with respect to the same aether. Similarly, if the earth's orbital motion happened to coincide with the aether in the winter, then all one would have to do would be to try again in the summer, when the earth would be traveling 65,000 m.p.h. in the opposite direction. Therefore, no matter how you view the pervasive ocean of aether, the earth and everything on it must be moving at a fairly rapid clip through this medium.
If the earth is moving through the aether, then it follows that there will be an aether "current" as experienced on the earth. This will be true even if the aether itself is completely calm and still in some absolute sense, just as a child can create an apparent "wind" even on a perfectly calm day by running through the calm air. The earth's motion within the figurative ocean of aether similarly will create the aether "current." (In the scientific jargon of the day, this relative motion was usually referred to as an aether "wind," employing the metaphor of motion through the air. I will call it an aether "current" to keep my own metaphors reasonably consistent.)
Therefore, any light emitted on earth will be traveling in some respect relative to this aether current -- either upstream, or downstream, or to some degree across the current.
Light waves traveling upstream in this aether current should appear to proceed more slowly than light waves traveling across the current or downstream. Vice versa, light waves traveling downstream should appear to proceed more quickly than light waves traveling across the current or upstream. In any event, there should be a difference in the speed of light, as measured on the moving earth, depending on how the light is traveling relative to the aether current. That is the nature of a wave.
With his interferometer, Michelson intended to detect this difference in the perceived speed of light, no matter how small that difference might be. To do so, he simply used a focused beam of light and split it with a mirror so that half the beam went one way, and the other half went off at a 90° angle, with both halves of the original beam still tightly focused on their new courses. Michelson then brought the two beams back together in such a way that each beam had traveled exactly the same distance when they were rejoined. The difference between the two halves of the beam was that one of the beams had traveled in one direction relative to the aether current, and the other had traveled in a perpendicular direction. Therefore, with the exception of two precise positions of the apparatus (at 45° to the aether current, both upstream and downstream), there would always be a difference in the motion of the light waves relative to the aether current. If either beam slowed down or speeded up in the slightest relative to the other beam, rejoining the two beams would create an interference pattern -- because the crests and troughs of the light waves would no longer match up exactly.
Because he had no idea in which direction the aether
current flowed, Michelson put his interferometer on a table top that could be
rotated. In this way, he could spin the entire apparatus and measure the
interference of the beams from any and all angles.
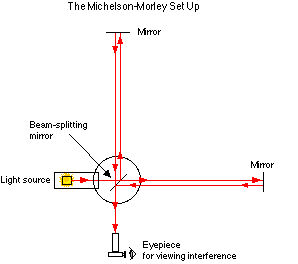
When Michelson announced his preliminary results, the scientific community was profoundly skeptical. Various objections were posed concerning Michelson's methods, so that Michelson was sent back to the laboratory with instructions to tighten up the experiment. Working with a new collaborator, E.W. Morley, Michelson improved the sensitivity and reliability of his interferometer. By 1887, Michelson and Morley were able to persuade the scientific community of the soundness of their approach and the exquisite sensitivity of their apparatus. The result of the experiment was that no interference was produced, regardless of the orientation of the interferometer. That is to say, there was no difference in the speed of a light wave traveling upstream, downstream, or across the current of its presumed medium, the aether.
The full implications of this experimental result are truly astonishing. As an aside, I will note that Einstein's special theory of relativity (1905) was prompted, in significant part, by the need to explain the results of the Michelson-Morley experiment. But, even apart from its leading to the revolutionary ideas of relativity, the Michelson-Morley experiment forced a confounded scientific community to conclude, very reluctantly, that there was no aether. None. Aether did not exist. And I hope that the reader can now appreciate the consequences which this conclusion had for the wave theory of light: light, apparently, was a wave without a medium!
"B-b-but," you object, "how can you have a wave without a medium? What is 'waving'?" Good question. Excellent question. Keep asking questions like that. I have no answer for you at this time, just as the scientific community had no answers in 1887.
Double slit experiments with electrons. [1] We now move on to electrons. Electrons are a very small, but very important, part of atoms. What is an atom? The theory of atoms began with the Greek philosophy of "atomism," expounded by Democritus of Abdera and his philosophical school. In its original form, atomism consisted, essentially, of the assertion that the universe is made up of solid things with substance, moving around in a void of nothingness. The things were called Atoms. (The void was called the Void.) This was not so much a "scientific" concept in our modern usage, as a philosophical concept. In the 19th century, this concept took on a new twist with the scientific assertion that all solid things with substance were composed of tiny particles, which again were called atoms. These 19th century atoms were thought to be the final, indivisible building blocks of nature. That is, according to the theory, if one were to pulverize and subdivide an object -- say a billiard ball -- it would finally be found to be a collection of tiny particles which could not be cut in half or in any way subdivided further. Through 20th century refinements, the things we now call atoms were determined to be composites of even tinier units. For our present purposes, we will be considering only the major divisions of the 20th century atom, which are: electrons, protons and neutrons. These can be isolated, examined, and handled individually with relative ease.
Now, Newton and Huygens could argue long and hard about whether light was a particle or a wave. After all, light was a mysterious phenomenon that couldn't be pinned down. For one thing, light always moved at the speed of light. You couldn't stop it and look at it. You could sort of feel it (as a sensation of warmth when you stepped out of the shadows on a summer day), but you couldn't exactly touch it. It is easy to see how reasonable minds might differ concerning light's fundamental nature. But nobody ever seriously questioned that when you had finished pulverizing a billiard ball, you would be left with solid little chunks of billiard ball. If the thing you started to pulverize was a solid, substantive thing, then whatever you are left with must be similarly solid and substantive. The billiard ball itself, in theory, is nothing more and nothing less than a large collection of these little units, so whatever properties the billiard ball has must come from its constituent parts. And you can only build a big, solid, substantive object by using little objects that are equally solid and substantive. Q.E.D.
The electron, when it was discovered in 1897, turned out to be an item that you could hold in your hand, figuratively speaking. It was possible to isolate a single electron. One lonely electron. And it could not be subdivided further, which is the acid test for a truly elementary unit. Electrons come in one unit and one unit only: the electron. Every electron is just like every other electron. There is no such thing as half an electron. And very soon after the discovery of the electron, the experimentalists got around to running these lonely electrons through the standard battery of tests. And these tests included the double slit experiment.
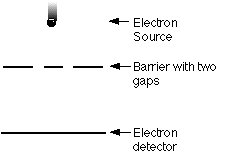
The set up for double slit experiments with electrons
is essentially the same as for double slit experiments with light. At least, the
diagram looks the same. Of course, where we used a simple projection screen as a
back wall for the light experiment, we now must use a sensitive electron
detector as the back wall for electrons. (This is not so different, since the
projection screen was serving as a "light detector" for the purposes
of the double slit experiment with light. We "detected" the light by
seeing the reflection off the screen, just like with a slide show or movie
screen.)
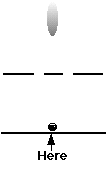
So let's keep sending these electrons through the
apparatus. The next one appears . . .
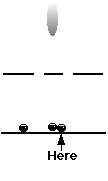And the next, 
Now, recalling what we know from the previous chapter
about the different ways that things can travel through a double slit, of what
does this remind us?
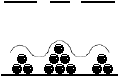
One key difference between this electron double slit experiment and Young's original experiment with light is that we cannot say that the experiment with electrons is completely and precisely consistent with wave motion -- nor that it is completely inconsistent with particle motion. How does one get an interference pattern when, one at a time, we take these little billiard balls which are electrons, and send them through the apparatus? At each step, we started out with one whole electron (there isn't any other kind of electron) -- which to all appearances is just like a little billiard ball; and we ended up with one whole electron which has the same appearance.
When we try to visualize what might be going on between the time we send the electron on its way and the time it hits the back wall, we get hopelessly muddled. Try to think of the initial motion of the electron as somehow starting a wave, like a pebble dropped in the wave tank. The metaphor just doesn't work for any number of reasons:
Why should the electron have started a wave in our double slit apparatus, rather than before, during or after the experiment? I.e., is there anything about our experimental set up that causes the electron to make a "splash"? Not that we know of.
What is the medium? If you think we had difficulty imagining what light's medium might be, just try to conceive of what an electron's medium might be. It's not easy. Eau de l'ectron?
In a wave tank, the pebble that starts the wave immediately sinks to the bottom of the tank and stays there; in a double slit experiment, the electron which "starts the wave" will later be found at the other end of the apparatus. No wave motion that we know of can accomplish this feat, which would completely erase the distinction between the instigating agent (the pebble) and the wave which, as far as we know, simply represents the transmission of the force of the falling pebble.
If we try to think of the electron as somehow "surfing" along the crest of the wave, we have to account for many oddities, like -- why would the instigating agent surf along in the direction of the double slits? how would this produce an interference pattern that would determine the location of the pebble/electron?
If the electron is more like a drop of water than a pebble, maybe the wave is like the splash of the water droplet itself and the wave is the splashed electron; but, how does the electron then reconstitute itself at the back wall? What happened to all the rest of the splashed electron heading off in different directions? And, considering that electrons always seem to come in whole units, how do we divide what seems to be indivisible?
In fact, the only thing about the electron double slit experiment that seems to have anything at all to do with waves is -- our statistical analysis of the result. Can it be a mere coincidence that our statistical analysis of the result happens to match exactly and precisely the statistical results that we obtain from wave motion?
Reexamining Young's original double slit experiment. Around about the turn of the century, the experimental scientists were making better and better measurements of light, which everybody knew was a wave, even if nobody could figure how it traveled without a medium. Now, a wave is a continuous function. It is a smooth curve. (Unless, of course, you mess around with it to produce a CD recording; but at the turn of the century, nobody had ever heard of a CD recording. The poor savages didn't even have cellular phones or computer games.) Nevertheless, even around the turn of the century, scientists were finding that some things about light occurred not continuously, but in jumps. And so the theorists theorized as follows: "Okay, if light does things in jumps, that says to me particles and not waves, so maybe light isn't a wave after all but is a particle." And they worked that into their calculations and they found that this supposition worked better in certain situations. It fit the results better. But then they had to ask themselves, well, what about Thomas Young's experiment? What about that result?
Eventually, the technicians developed extraordinarily sensitive instruments -- instruments capable of detecting a single pulse of light energy, or even half of a pulse. These instruments were much, much more sophisticated than the simple projection screen that Thomas Young used as his light detector. And so, just to see what would happen, they repeated Young's experiment using these hypersensitive light detectors, with a light so dim that the light detectors could make very fine measurements of what was happening at the back screen.
These fine measurements revealed something surprising about the interference pattern of light being detected at the back screen. The "wave-like" interference pattern was neither smooth nor continuous. The light detectors at the back screen were registering exactly one unit of light energy at a time -- never more, never less. A-and the "wave interference pattern" consisted merely of a build-up, over time, of the accumulated units of light energy registered by the light detectors-- just like with the electrons. There was no interference pattern at first, only scattered and seemingly random "hits" at the light detector; but, eventually, these scattered and random hits built up into the stripes of light that Thomas Young had seen. Young had not recognized this process because he was throwing billions and trillions of light energy units through the double slits and on to the projection screen at all times. By the time he blinked his eyes (much more quickly than that, actually), the "interference pattern" was a fait accompli.
In fact, it turned out that light, the
mysterious and ephemeral phenomenon, was behaving in exactly the same way as
electrons, those solid little remnants of the pulverized billiard ball. But
that hardly helps us, because the electrons themselves are behaving in a very
odd fashion -- starting as particles that seem fairly straightforward, and
ending as particles that happen to distribute themselves according to wave
interference principles.
Trying to examine the process. We sure would like
to know what is going on between the time we send the electron (or a bit of
light, for that matter) on its way, and the time it registers at the detector.
First, we would like to know how the electron got through the slit. The
possibilities are: 1) the electron went through the left slit; or 2) the
electron went through the right slit; or 3) the electron went through both
slits. For the sake of logical rigor, we should add the possibility that 4) the
electron went through neither slit (that is, it found some other way to
get to the back wall). Now, one problem with possibility number 3 -- a single
electron going through both slits -- is that, in nature, there is no such thing
as half an electron. So if we found half an electron at both slits, we would
have something really new; but that has to be a distinct possibility,
considering that, in order to create the apparent interference pattern,
something would have to radiate from both slits.
How are we going to find out? Well, we are going to
put an electron detector at each slit. The electron detectors at the slits will
be devices to keep watch over the passage through the slit. Every time an
electron (or part of an electron) goes through, the detector will give a holler,
"Hey, an electron (or part of an electron) just went through." In this
way, we will be able to learn something about how the electrons get through the
barrier in a double slit experiment.
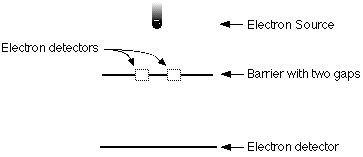
So, again we must ask ourselves: how can we get an interference pattern when we send just one electron through the apparatus, it goes though one slit or the other as just one electron, and it registers at the back wall as just one electron. Even if the electron was in some respect "wave-like," we still need two wave-like things to create an interference pattern.
Here's the scary part.
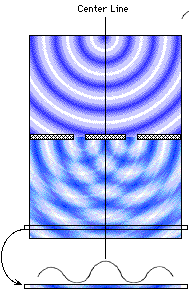
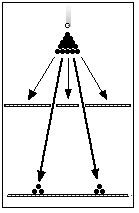
We record our results from this modified double slit set up, just like we did before. At the end of our long and frustrating day, we tally the results, just like we did before. The results look like this:
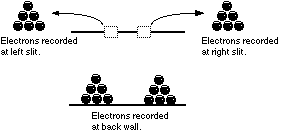
This is not an interference pattern.
This is a clumping pattern in line with the slits.
A clumping pattern in line with the slits is typical of simple particle motion.
Contrast this with the initial results from sending electrons through the apparatus (p. xx).
What happened to our interference pattern? It went away. Instead of an interference pattern, with all of its problems of interpretation, we now have a straightforward particle distribution. By detecting particles at the slits, we have changed the result at the back wall. Somehow, detecting particles at the slits has had two effects: (1) it has caused there to be particles at the slits despite the fact that, based on our previous results, we were expecting something (who knows what) with a wave-like nature; and (2) it has caused the particle that we presumably started out with to behave entirely like an innocent little particle from start to finish.
Why?
We would like to think that the particle detectors at the slits are affecting the passage of the electron -- perhaps deflecting it, or modifying it's path, or in some other way influencing the experiment. We could accept such an explanation. But that does not seem to be the case. A series of experiments have been conducted to test just such a hypothesis, and the results are uniformly negative. I will quickly run through some of the more ingenious attempts to isolate and remove any possible influence stemming from the detectors located at the slits.[2]
1. Turn off the electron detectors at the slits. Suppose we take our modified double slit set up -- with electron detectors at the slits -- and leave everything intact. But, we will conduct the experiment with the electron detectors at the slits turned off, so that we will not actually detect any electrons at the slits.
The result upon analysis: an interference pattern at the back wall. So it seems that mere passage through the electron detectors at the slits does not affect the electron, so long as those electron detectors are not functioning.
2. Leave the electron detectors on, but don't gather the information. Suppose we take our modified double slit set up -- with electron detectors at the slits -- and still leave everything intact. And we will keep the electron detectors at the slits turned on, so that they will be doing whatever they do to detect electrons at the slits. But, we will not actually look at the count of electrons at the slits, nor will we record the count at the slits in any way, so that we will not be able to obtain any results from these fully-functioning electron detectors.
The result upon analysis: an interference pattern at the back wall. So it seems that the electron detectors located at the slits do not themselves affect the electron, even when the equipment is fully functioning and detecting (in a mechanical sense) the electrons, so long as we don't obtain the results of these measurements.
3. Record the measurements at the slits, but then erase it before analyzing the results at the back wall. Suppose we take our modified double slit set up -- with electron detectors at the slits -- and still leave everything intact. And we will still keep the electron detectors at the slits turned on, so that they will be doing whatever they do to detect electrons at the slits. And we will record the count at the slits, so that we will be able to obtain the results. But, we will erase the data obtained from the electron detectors at the slits before we analyze the data from the back wall.
The result upon analysis: an interference pattern at the back wall. Notice that, in this variation, the double slit experiment with detectors at the slits is completed in every respect by the time we choose to erase the recorded data. Up to that point, there is no difference in our procedure here and in our initial procedure ([pp. 15-17]), which yielded the puzzling clumping pattern. Yet, it seems that if we, in a sense, retroactively remove the electron detectors at the slits (not by going back in time to physically remove them, but only by removing the information they have gathered so that it is not available from the time of the erasure going forward into the future), we can "change" the results of what we presume is a mechanically complete experiment, so far as those results are determined by a later analysis, to produce an interference pattern instead of a clumping pattern. This is mind-boggling.
4. Arrange the experiment so that we can make an arbitrary choice at
some later time, after the experiment is "complete," whether or not to
use the information gathered by the electron detectors at the slits.
Suppose we take our modified double slit set up -- with electron detectors at
the slits -- and still leave everything intact. And we will still keep the
electron detectors at the slits turned on, so that they will be doing whatever
they do to detect electrons at the slits. And we will record the count at the
slits, so that we will be able to obtain the results. But (this gets a little
complicated), we will
(1) mix the data from the slits with additional, irrelevant garbage data, and
record the combined (and incomprehensible) data;
(2) design a program to analyze data coming from the slits in one of two ways,
either
(a) filtering out the garbage data so that we will be able to
obtain clean results of electrons going through the slits, or
(b) analyzing the mixed-up data so that we will not be
able to obtain the results of electrons going through the slits; and
(3) leave it up to a visiting politician which way we actually analyze the data
from the slits.
The result upon final analysis by method (2)(a): a
particle clumping pattern appears from the data.
The result upon final analysis by method (2)(b): an
interference pattern appears from the data.
So it seems that an arbitrary choice (represented by the politician who has no personal interest in the experiment) made hours, days, months, or even years after the experiment is "complete," will change the result of that completed experiment. And, by changing the result, we mean that this arbitrary, delayed choice will affect the actual location of the electron hits as recorded by the electron detector at the back wall, representing an event that was supposed to have happened days, months, or even years in the past. An event that we suppose has taken place in the past (impingement of the electron on the detector) will turn out to be correlated to a choice that we make in the present. Imagine that.
The proverbial tree has already fallen in the forest, and we can later choose whether or not to listen. And if we choose to listen then the falling tree will have made a noise, and if we choose not to listen then the falling tree will not have made a noise.
What is the difference? It turns out that, so far as experimentalists have been able to determine, the difference is not whether electrons were run through an electron detector at the slits. It turns out that, so far as experimentalists have been able to determine, the difference is whether the analysis of the results at the back wall is conducted when information about the electrons' positions at the slits is available, or not.
In searching for the wave-like phenomenon that must, it simply must be taking place in the unmodified electron double slit experiment, the theorists are left with the equivalent of a parent's worst nightmare: you hear the screaming and pounding and crashing of broken lamps from the child's room; but every time you open the door . . . there sits the innocent little darling like an angel, eyelashes batting, smiling beatifically (probably reading the Bible), "Yes, Mother/Father, can I help you with something?" You close the door in bewilderment, and immediately the racket starts up again. Well, the theorists know that there is something wave-like going on. They can see the indisputable evidence of waves in the interference pattern and in their extraordinarily precise predictions based on a wave model. But, every time they look for the wave itself -- there is no wave, only a particle. And, perversely, all evidence of waves simultaneously disappears!
The measurement effect. With sublime understatement, this phenomenon is referred to as "the measurement effect." When we measure (or detect, or see, or quantify, or determine, or otherwise gain knowledge of) something at the quantum level, the very act of measurement will have an effect on the thing itself. To all intents and purposes, the act of a sentient being in seeking a measurement will cause the thing to have a property which can be measured, and thereby produce a definite property that can be measured.
Since around 1927, the standard quantum mechanical explanation for the difference between results in the double slit experiments particularly, and for the measurement effect generally, is that in one set of experiments, we know (or more precisely, we can in principle know)[2a] which slit the electron went through; and in the other set of experiments, we don't know (i.e., we cannot know even in principle)[2a] which slit the electron went through. This conclusion is one facet of the "Copenhagen interpretation" of quantum mechanics (so named because it was developed by Niels Bohr's institute located in Copenhagen, Denmark), which represents the closest thing to a consensus among physicists for the last seventy years or so.
The difference is whether we know. The difference is whether we choose to have the information available.
If we demand to know which slit the particle went through, then a particle must appear at one slit or the other so that we will have an answer to our question; and so our curiosity has caused there to be a particle at one of the slits, and now there is a particle; and if there is a particle at one slit or the other, it must obey the rules for particle motion, and so it does.
Conversely, if we do not demand to know which slit the particle went through, no particle need appear at either slit; and so we have not caused there to be any particle, and now there is no particle; and if there is no particle at either slit, the system remains free to roam the universe in whatever form seems most pleasing to itself.
And all of this is determined at the time we demand the knowledge, not at the time we institute any mechanical processes for obtaining the information.
Who cares about a bunch of electrons in the laboratory?
Tell me something I can use in the real world, like my kitchen. Recall
that, according to the most successful scientific theory of all time (quantum
mechanics), all quantum units exhibit the properties we have seen in the double
slit experiments. Indeed, we have already seen that light units and electron
units -- two phenomena that, at first blush, seem to have nothing to do with
each other -- behave in exactly the same way. Recall further that, according to
this same theory, everything in the entire universe is made up of quantum units.
That being the case, what exactly does the skeptic have in mind when he or she
speaks of the "real world" as though it were somehow different from a
bunch of electrons in the laboratory? What we are seeing in the laboratory is
the "real world"; it is, in fact, the real "real
world," stripped of appearances created by the vast number of individual
quantum observations we must make whenever we observe anything in our
day-to-day, ground level lives. The double slit experiment with light seemed
fairly straightforward when we were forced to observe billions and trillions of
quantum units all at once; but it turned out that each of those multiple
observations actually was following the precise rules of quantum mechanics,
rather than our "intuitive" rules of how things should behave,
based on the gross observations of our day-to-day experience.
The task of "scaling up" the results of quantum mechanical experiments -- from individual light units and individual electron units to the "real world" of our five biological senses -- is largely a philosophical one. Scientific philosophers (called "theorists"), have proposed a number of good mechanisms to explain why our observations at the "macroscopic" level (i.e., the world of relatively large things that we see around us) should seem so different from the results of our measurements at the "microscopic" level of almost unimaginably small individual quantum units. But this effort is directed mainly toward the difference in appearances, not to any difference in the actual processes. This is the same intellectual effort required when attempting to explain why the earth appears to be flat-ish when, in fact, it is demonstrably round-ish. In quantum theory, there is no essential difference between the electron and, say, the toaster oven in your kitchen. Each can be described in terms of a "wave function" which will make predictions just as successfully for the toaster oven as for the electron. The difficulty in sending a toaster oven through a double slit apparatus is experimental, not theoretical. That is to say, it is difficult enough to design a double slit experiment using single units of something as simple and fundamental as an electron; but it is a practical impossibility to design a double slit experiment using objects as large and composite and complex as a toaster oven, as we shall see.
The experimentalists have never stopped trying to scale up their experiments to ever larger and more complex collections of quantum units. We have discussed the most basic experiments, using light units and electron units, both of which are truly fundamental and indivisible according to current theory (and, therefore, utterly and ultimately simple). Proton units, which as noted earlier are thought to be composite units made up of three sub-units, have been subjected to the double slit tests with the same results as light units and electron units. Recently, helium atoms -- consisting of two electron units, two proton units and two neutron units all bound together -- have been put through the double slit experiment with the same results. Even more recently, 60 atoms of carbon have made the journey in exactly the same way.[3] It is estimated that with current technology, objects the size of viruses can be put through a double slit experiment and will behave in just this way.[4]
Quantum theory says it would be possible to put a toaster oven through the double slits in the same manner, except for a small hitch -- the amount of time it would take for the toaster oven's "wave function" to traverse the apparatus. As the object becomes more and more complex, it must travel more and more slowly through the apparatus. A toaster oven is made up of billions and trillions and quadrillions of quantum units. At that level of complexity, travel through the double slit experiment must be very slow indeed for the quantum effects to become manifest: if the toaster oven had started its journey at the beginning of time, many billions of years ago, it would not yet have made it through. Apart from that experimental difficulty, quantum mechanics dictates that the toaster oven would distribute itself according to the wave model if no detectors were giving information at the slits, and according to the particle model if detectors were giving information (which was being read) at the slits.
In this matter of scaling the results of experiment, at least, quantum theory does not contradict logic or experience. Let us return to the logical relationship of the part to the whole, as we discussed in the context of the original "scientific" concept of an atom (see p. xx, above). However, instead of reasoning downwards from what we think we know about a billiard ball to deduce the properties of its constituent atoms, we may now reason upwards from what we know about the behavior of the electron, proton, and neutron units to deduce the properties of the conglomerate billiard ball that is built up from them. That is, if the units you start out with are unsolid, nonsubstantive phenomena, which depend for their very form and existence on your seeking and gaining knowledge of their locations, then whatever you build with these units must be similarly unsolid and nonsubstantive. The billiard ball itself, in theory, is nothing more and nothing less than a large collection of these little units, so whatever properties the billiard ball has must come from its constituent parts. And the only thing you can build using little units that are unsolid and nonsubstantive, is a big unit that is equally unsolid and nonsubstantive. Q.E.D.
Quantum theory's prediction about the behavior of a toaster oven (or a billiard ball) in a double slit experiment (given the right experimental conditions) is more than an exercise in logical reasoning; it is a necessary consequence of the mathematics of the quantum processes. Since every other prediction ever made by quantum theory has proved correct, we have little choice but to accept this prediction, too, as correct. With this in mind, I urge you now to go back over the double slit experiments described in this chapter, and to follow them along step-by-step until you are shocked. Then, pick up a toaster oven, hold it in your hand, and ask yourself, "Just what exactly is this that I appear to be holding?"
| 1 [Back] |
Double slit experiment with electrons: A. Tonomura, J. Endo, T. Matsuda and T. Kawasaki, “Demonstration of single-electron buildup of an interference pattern”, Am. J. Phys. 57, 117 (1989). C. Jönsson, Zeitschrift für Physik 161, 454; C. Jönsson "Electron diffraction at multiple slits," Am. J. Phys. 42, 4-11 (1974). P.G. Merli et al., Am. J. Phys. 44, 306-7 (1976). See "The double-slit experiment," Physics World (Sept. 2002, at p. 15; supp. May 2003) (discussion of double slit in general and electron double slit in particular, with comments from Tonomura and Merli), available at http://physicsweb.org/articles/world/15/9/1. See also Hitachi website, http://www.hqrd.hitachi.co.jp/em/doubleslit.cfm, and especially http://www.hqrd.hitachi.co.jp/em/movie.cfm, for striking photographs and video from the Tonomura experiment. |
| 2 [Back] |
These situations are principally derived from the phenomenon known as "delayed choice," proposed by John Wheeler, see Quantum Theory and Measurement, J.A. Wheeler and W.H. Zurek, eds. Princeton Univ. Press (1983). The QM predictions have been experimentally realized and verified by, e.g., V. Jacques, et al., "Experimental realization of Wheeler's gedankenexperiment," Science 315 966 (2007), e-print at http://www.arxiv.org/abs/quant-ph/0610241 ; A.G. Zajonc et al., Nature, 353, 507 (1991); P.G. Kwiat et al., Phys. Rev. A 49, 61 (1994); T.J. Herzog et al., Phys. Rev. Lett., 75, 3034 (1995); T.B. Pittman et al., Phys. Rev. Lett., 77, 1917 (1996). The Jacques experiment is described in Physics World, "Photons denied a glimpse at their observer" (Feb. 15, 2007), http://physicsworld.com/cws/article/news/27106 . At least one quantum eraser double slit experiment has been accomplished with electrons. I. Neder, et al., "Entanglement, Dephasing, and Phase Recovery via Cross-Correlation Measurements of Electrons," Phys. Rev. Lett. 98, 036803 (2007-Jan-19), e-print at http://arxiv.org/ftp/cond-mat/papers/0607/0607346.pdf. This is said to be the electron equivalent of "ghost interference" as reported by D. Strekalov, et al., "Observation of two-photon 'ghost' interference and diffraction," Phys. Rev. Lett. 74, 3600 (1995), which is nicely described in P. Chingangbam, et al., "Two particle ghost interference demystified," e-print at http://arxiv.org/PS_cache/quant-ph/pdf/0502/0502162v1.pdf. See also Qureshi T., et al., "Quantum Eraser Using Spin-1/2 Particles" (2005), e-print at http://arxiv.org/PS_cache/quant-ph/pdf/0501/0501010v1.pdf. The experimental realizations of delayed choice of which I am aware have all been accomplished with photons. This is mainly due to the ingenious scheme developed by Marlan O. Scully which employs entangled pairs of photons to accomplish which-path measurement 1) with no interaction; and 2) with the ability to manipulate the which-path information. M.O. Scully and K. Drühl, Phys. Rev. A 25, 2208 (1982). For pedagogical purposes, I have continued to use electrons as the quantum units under discussion. With recent successes in achieving entanglement among atoms, it seems likely that these experiments may be repeated in the near future with various quantum units of matter (if this has not already been achieved). QM being what it is, there is no question but that the results will be consistent with those obtained with photons. Summary of the basic idea of delayed choice experiments is available athttp://www.bottomlayer.com/bottom/basic_delayed_choice.htm For an elegant delayed choice experiment, see Yoon-Ho Kim, et al., "A Delayed Choice
Quantum Eraser", Phys.Rev.Lett. 84 (2000) 1-5 http://xxx.lanl.gov/pdf/quant-ph/9903047.
Commentary on this experiment is available at Another excellent experiment is reported at G. Scarcelli, Y. Zhou and Y. Shih (Dep't of Physics, Univ. of Maryland). "Random Delayed-Choice Quantum Eraser via Two-Photon Imaging." (Dec. 22, 2005) http://arxiv.org/abs/quant-ph/0512207 Recently, a group advised by Alain Aspect reported a successful delayed-choice experiment with single photons and direct intervention by the experimenter. V. Jacques, et al., Experimental realization of Wheeler's delayed-choice GedankenExperiment (Oct. 31, 2006), e-print http://www.arxiv.org/abs/quant-ph/0610241 Paul Kwiat and Rachel Hillmer describe "A Do-It-Yourself Quantum
Eraser" in the May 2007 edition of Scientific American <click
here>. All you need is a laser pointer and some polarizing
filters, and they even tell you where to get the polarizing filters.
If I were still in high school, this would be my science project! |
| 2a [Back] |
It is not necessary to see or comprehend the information that is available. The experimenter cannot make information go away by not looking at it. If the information is available, it will be reflected in the measurement outcome. |
| 3 [Back] |
M. Arndt, et al., "Wave-particle duality of C60" Nature
401, 680-682 (1999). Summarized at "Wave-particle
duality of C60 molecules," http://www.quantum.at/research/molecule-interferometry-foundations/wave-particle-duality-of-c60.html |
| 4 [Back] |
L. Hackermuller, et al., "Decoherence in a Talbot Lau
interferometer: the influence of molecular scattering" http://www.arxiv.org/pdf/quant-ph/0307238 |
 The Reality Programby Ross Rhodes  The Notebook of Philosophy & Physics |