The Reality Program: Chapter 3

Chapter Three

The Uncertainty Principle
Quantum Properties, and More on the Measurement Effect

Tink was not all bad: or, rather, she was all bad just now, but, on the other hand, sometimes she was all good. Fairies have to be one thing or the other, because being so small they unfortunately have room for one feeling only at a time. They are, however, allowed to change -- only it must be a complete change.

J.M. Barrie, Peter Pan

Properties. In the last two chapters, we have spoken of "properties" of waves and particles in our experience, and "properties" of quantum units. Let us try to define the word "property" for our purposes. In a very general sense, a "property" is something about an object or a phenomenon that you can measure or describe. Weight, height, color, speed, symmetry, density, location, temperature, wetness, and so forth, are all "properties" in this sense. 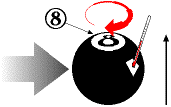If I hold a billiard ball, say the 8-ball, in my hand, I can start to tell you something about its properties: it is spherical; it weighs about 6 ounces; it is mostly black; it has the number 8 painted on it. These are properties that we think of as being part of a description of this particular billiard ball; that is, if I set the billiard ball down, I believe I can still say that it weighs about 6 ounces, and is mostly black. What is more, if I had put it down so that I couldn't actually see the number 8, I still would be prepared to go way out on a limb and say it had the number 8 painted on it. Why should the number change? The painted number 8 is one of the properties that I think of as defining this particular billiard ball.

I can describe other properties of the billiard ball, variable properties that might change over time. For example, I can pick it up and tell you that it is located in my hand. That will certainly change if I put it down. I could tell you that the painted number 8 is positioned at the top of the billiard ball as I hold it. That, too, will change if I turn it upside down. If I put it down on the table and give it a spin, I can tell you it is spinning clockwise when viewed from above; if I stop it and spin it the other way, I could tell you it is spinning counter-clockwise.

Sometimes we measure properties directly, which is what I have been doing so far - looking at it and seeing the visible properties, or holding it and feeling the weight. On the other hand, sometimes we measure properties indirectly. Suppose I spun the 8-ball so fast it was a blur and I couldn't tell if it was spinning clockwise or counter-clockwise. There are lots of ways I could still measure which direction it was spinning. For example, I could watch it head straight for the bumper, and then see whether it bounced off to the left or to the right; if to the left, then it was spinning clockwise; if to the right, then it was spinning counter-clockwise. In this example, I am measuring the spin direction indirectly, by observing how the billiard ball behaves and using my rudimentary knowledge of physics to deduce that the behavior (a deflection in the way it rebounds) is caused by spinning in a certain direction.

By making many observations (measurements) of the billiard ball, I can give you a fairly complete description of the 8-ball and what it is doing at any given time. Here is an exercise in describing many properties of the billiard ball:

Its existence property is: existing (as opposed to all the billiard balls the manufacturer plans to make next year)

Its shape property is: spherical

Its weight property is: 6 ounces

Its color property is: black

Its number property is: 8

Its number orientation property is: at the top

Its spin property is: spinning

Its spin direction property is: clockwise

Its location property is: on the table

Its temperature property is: about room temperature

Its motion-with-respect-to-the-table property is: standing still (but spinning)

And so on. After a while, I can give you a very complete description of this billiard ball. And even if it starts to move across the table (perhaps because of the spin), so that its motion-with-respect-to-the-table property changes and its number orientation property changes; and even if it falls off the table so that its location property changes, and it slows down and stops spinning - I could still pick a single instant and tell you all about the billiard ball as it existed at that moment.

Predictability and certainty in our day-to-day, ground level lives. I mentioned before that when I put the 8-ball down, I will still believe it has an 8 painted on it, even if I can't see the number because of the way I put it down. The same is true of the shape property and the weight property and the color property. Once I've looked at it and felt it, I can put it down and close my eyes and, depending on my memory, give you what I think is an accurate description of the billiard ball.

Perhaps the most basic of these properties of which I am certain is the existence property. If I put the ball down on the table and then turn my back, I believe it will continue to exist. I turn around again, and sure enough it is still there, so this belief is reinforced. Having held it in my hand, I will stubbornly continue to believe it exists even if it is not there when I turn around again. In fact, if it is not there when I turn around again, I will speculate that it must have fallen off the table, so I will look around on the floor; or I will call out to my children and ask whether one of them has taken it. If all else fails - that is, if I check and the room was locked, and there is nothing on the floor, and there aren't any piles of papers that it could be under, and so forth - I will probably begin to wonder whether I saw it at all, or whether I really put it on the table just now or perhaps I am remembering something I did yesterday. In short, I will probably question my own sanity rather than consider that the billiard ball may have simply "disappeared" into nonexistence. I am that sure of the continued existence of things. Once we have passed the age of eight or nine, we don't believe for an instant that a magician can make something disappear; we may be impressed with the cleverness of the trick, but it's still just a trick, and we know that because we know that things do not actually "disappear."

We live our lives according to a kind of "certainty principle" in this regard. For the most part, we expect that once we have measured a property, it will stay measured unless and until something changes it. However, we have already seen that quantum mechanics does not always conform to our expectations.

The uncertainty principle in quantum mechanics. As with all aspects of QM, the uncertainty principle is not a statement of philosophy, but rather a mathematical model which is exacting and precise. That is, we can be certain of many quantum measurements in many situations, and we can be completely certain that our results will conform to quantum mechanical principles. In QM, the "uncertainty principle" has a specific meaning, and it describes the relationship between two properties which are "complementary," that is, which are linked in a quantum mechanical sense (they "complement" each other, i.e., they are counterparts, each of which makes the other "complete"). Put simply, the relationship is this:

For any two complementary properties, any increase in the certainty of knowledge of one property will necessarily lead to a decrease in the certainty of knowledge of the other property.

Uncertainty in properties subject to variation. The uncertainty principle was originally thought to be more statement of experimental error than an actual principle of any great importance. When scientists were measuring the location and the speed (or, more precisely, the momentum) of a quantum unit - two properties which turn out to be complementary - they found that they could not pin down both at once. That is, after measuring momentum, they would determine position; but then they found that the momentum had changed. The obvious explanation was that, in determining position, they had bumped the quantum unit and thereby changed its momentum. What they needed (so they thought) were better, less intrusive instruments. On closer inspection, however, this did not turn out to be the case. The measurements did not so much change the momentum, as they made the momentum less certain, less predictable. On remeasurement, the momentum might be the same, faster, or slower. What is more, the range of uncertainty of momentum increased in direct proportion to the accuracy of the measurement of location.

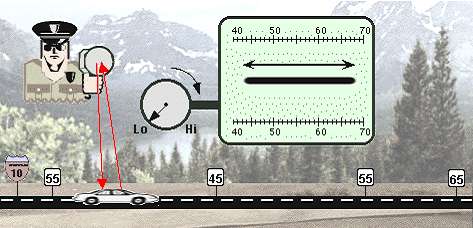
The uncertainty principle describes the behavior of quantum units as observed under laboratory conditions. As we have seen in the previous chapter, the behavior of quantum units often seems to defy common sense; and because the uncertainty principle describes this seemingly illogical behavior, the principle itself seems to defy common sense. In order to get some idea of what the uncertainty principle "means," let us see how it might apply to a common situation involving measurement of both momentum and position, to wit, the speed of a car and its location along a highway.

The parable of the conscientious traffic cop. Imagine a state trooper on traffic assignment. He has a radar gun which can be adjusted for more or less accuracy, depending on the need. He has set up a speed trap along a section of the interstate which borders a rural and urban area, and which has some construction in progress. Because of the differing zones and the construction, the speed limit along this stretch of road changes from 65 m.p.h., to 55, to 45, and back to 55, all within a space of, say, 200 yards.

Trooper with radar set to low accuracy

When the trooper first uses his radar gun, he sets it only to rough accuracy, and trains it on a car that seems to be in the construction zone. The radar shows that the car is going somewhere between 40 and 70 m.p.h. Obviously, this is not good enough to write a ticket, because if the actual speed is in the lower end of this range (40 m.p.h.), then the car is not speeding in the 45 m.p.h. construction zone.

Trooper with radar set to medium accuracy

For the next car, the trooper increases the accuracy of the radar, and he gets a reading of 47 to 63 m.p.h. However, it seems that this car might have been outside of the construction zone at the time of the measurement, so that the applicable speed limit might be 55 m.p.h., so this is still not good enough.

Trooper with radar set to high accuracy

The trooper increases the accuracy again, and gets a reading of 52 to 57 m.p.h. However, now he can't tell if the car was in the construction zone (45 m.p.h.), or the urban speed zone (55 m.p.h.), or even possibly the rural zone (65 m.p.h.). He still can't write the ticket.

When the trooper finally zeros in on a car that is going precisely 54.5 m.p.h. according to the radar gun, he can't even swear that it is in his state.

Expressing the uncertainty principle as a mathematical relationship. The dilemma faced by the state trooper in trying to measure both the speed and location of the car is the same dilemma faced by the early experimentalists in trying to measure both the speed (momentum) and location of quantum units. In 1925, the German scientist Werner Heisenberg conducted a mathematical analysis of the position and momentum of electrons. His results were surprising, in that they showed a mathematical incompatibility between the two properties. Briefly, the math showed that if you try to relate these two properties, you are left with a logical inconsistency: Property "p" (position) times Property "m" (momentum) equals some number; but Property "m" times Property "p" does not equal the same number. In mathematical terms, the properties are noncommutative. The two numbers, which should be the same, come out different because of the way they are calculated in a matrix of the quantum unit's properties. This was an unusual result for mathematics. We are used to multiplication which is commutative, which means that if four times three equals twelve, then three times four also equals twelve, it doesn't matter which way you put it. But in the mathematics of quantum properties, it is as if four times three equals twelve, but three times four equals fifteen, or some other number (which doesn't make any sense).

With a little more fiddling, Heisenberg was able to state that there was a mathematical relationship between the properties p (position) and m (momentum), such that the more precise your knowledge of the one, the less precise your knowledge of the other. This "uncertainty" followed a formula which, itself, was quite certain.[1] Heisenberg's mathematical formula accounted for the experimental results far, far more accurately than any notion of needing better equipment in the laboratory. It seemed, then, that uncertainty in the knowledge of two complementary properties was more than a laboratory phenomenon - it was a law of nature which could be expressed mathematically.

The uncertainty principle with regard to position and momentum has definite and mathematically predictable consequences for quantum units such as electrons, which we will discuss later in this book. For now, just try to imagine that the state trooper, by increasing the accuracy of his radar gun, has caused the car on the interstate to stretch out between the different speed zones. That would be quite a "measurement effect." Yet, it is in almost this way that getting a good fix on the momentum of, say, an electron unit actually causes a spreading of the range of possible locations in which we may expect to find the electron unit when we ask for (measure) its location. Vice versa, by confining an electron unit to a smaller and smaller space in which it can be located (i.e., by determining its position more and more precisely), the range of its possible momentum becomes larger and larger. It will still have just one momentum when we get around to measuring it, but that momentum will turn out to be a number within a wider and wider range. Every once in a while, following a precise set of probabilities, such a "confined" electron unit will suddenly exhibit a huge momentum, because such a large momentum has become mathematically possible due to the confinement. That is to say, larger and larger energies (momentums) become a possibility for the electron because of the increase in the certainty of our knowledge of its position - not because it has been bumped or energized in any way. And since these larger energies have come to be included in the range of possibilities, the electron will actually have such a large energy every so often, according to the relative likelihood of that energy level.

Uncertainty in complementary properties that are "quantized." Recall that one distinguishing feature of quantum units is that many of their properties come in whole units and whole units only. That is, many quantum properties have an either/or quality such that there is no in between: the quantum unit must be either one way or the other. We say that these properties are "quantized," meaning that the property must be one specific value (quantity) or another, but never anything else. When the uncertainty principle is applied to two complementary properties which are themselves quantized, the result is stark. Think about it. If a property is quantized, it can only be one way or the other; therefore, if we know anything about this property, we know everything about this property.

There are few, if any, properties in our day to day lives that can be only one way or the other, never in between. If we leave aside all quibbling, we might suggest the folk wisdom that "you can't be a little bit pregnant." A woman is either pregnant, or she is not pregnant. Therefore, if you know that the results of a reliable pregnancy test are positive, you know everything there is to know about her pregnancy property: she is pregnant.

What would be the consequence, according to the uncertainty principle, of knowing everything about one complementary property that was quantized? Well, the consequence would be that, as a law of nature, we then would know nothing about the other complementary property. At this point in the discussion of the uncertainty principle, analogy from our day to day lives fails us. Can we imagine that, by gaining the results of a pregnancy test, we lose other knowledge? I, for one, am unable to devise a suitable illustration. The very concept is alien. By our logic and experience, gaining knowledge of the results of the pregnancy test must increase the sum total of our knowledge. We add this knowledge to all the other things we know about the woman, and our total knowledge of her condition increases. Can we imagine instead that, by learning whether a married woman is pregnant, we thereby no longer know whether she is married? Yet, this would be the effect if marital status and pregnancy were complementary properties, and we applied the uncertainty principle to knowledge of them.

As you can see, the uncertainty principle leads to some thorny conceptual problems when we try to use our logic and experience to visualize what is going on in the quantum realm according to our intuitive "certainty principle," i.e., our general sense that once we are certain of something we can file it away as a fact and move on to the next investigation. Therefore, let us continue to talk in parables. Let us imagine that there are objects in our day-to-day, ground level lives that behave according to quantum principles. I caution you that playing out such a scenario will not help you to relate quantum phenomena to the world of your experience. At best, it will impress upon you that quantum phenomena are entirely different from the things and objects you know and love.

The Uncertainty Problem, or, The Parable of the Quantum Grapes

Background and definitions. The New York Times has just reported in its Tuesday Science Times section that the United States Department of Agriculture, working with the President's scientific advisors, has announced the discovery of a new kind of fruit: "quantum grapes." These (strictly hypothetical) quantum grapes are much like ordinary grapes, except that they behave in some respects like the quantum units scientists have been studying for the past 100 years or so - things like electrons and photons and neutrinos and protons and everything else of which the universe is comprised.[2]

According to The New York Times (in our hypothetical), these newly discovered "quantum grapes" come in two and only two varieties: green grapes and purple grapes. Every green quantum grape is exactly the same color, shade and hue as every other green quantum grape; and every purple quantum grape is exactly the same color, shade and hue as every other purple quantum grape.
Both varieties are found in one of two and only two positions: stem-up and stem-down. There are no other variations in stem position. No quantum grape has ever been found with a stem position at the side or anywhere else other than exactly stem-up or exactly stem-down.
To the naked eye, quantum grapes appear as gray blobs. To determine the properties of a particular quantum grape, the farmers and scientists have to put on special glasses.
One pair of special glasses allows you to see the quantum grape's color; but, unfortunately, these glasses blur the outline of the grapes so much that you can't see any stem when you are looking at the color.

The other pair of special glasses allows you to see a sharp outline of the quantum grape's stem; but, unfortunately, these glasses completely wash out the color.

To complete our hypothetical, let us imagine that we have jobs, and that we have a boss. Our boss doesn't know much about agriculture, and even less about quantum mechanics, but she does read the Science Times section, and it's around lunchtime, and she has something of a taste for the exotic. Hence our immediate problem: the boss has demanded that we bring her a bunch of quantum grapes that are green, with stems at the top. To the boss, this seems like an entirely reasonable request. What is more, the boss says we had better be darn certain that we bring her the right kind of quantum grapes.

Going about our task using our native intelligence and common sense. After a little research, we pull a few strings and obtain a supply of quantum grapes. To our unaided eyes, they all appear gray with no stems. By using the two pairs of special glasses that came with the grapes, we confirm that each quantum grape has a color, green or purple; and that each quantum grape has a stem, oriented either exactly stem-up or exactly stem-down.

We quickly discover how to separate the green from the purple grapes, using a simple color separator machine. We also can separate the stem-up from the stem-down grapes, using an equally simple stem-direction separator machine. With these tools, we are confident that we can satisfy the boss. Our plan is this: using our stem-direction separator machine, we will first sort our supply of quantum grapes according to stem direction; then, using our color separator machine, we will sort the stem-up grapes according to color. We can't think of any reason in the world why we should not then have a pile of quantum grapes, with stems at the top, that are green. These we can take to the boss. Let's see how this plays out, referring to the accompanying diagrams.

1. Testing the Equipment. Remember that the boss has demanded that we be absolutely certain of our result, and so we need to be absolutely certain of our equipment. Therefore, in figure 1.1, we begin with a bunch of quantum grapes (1) about which we know neither color nor stem direction. We run them through our stem direction separator (2) to determine which way their stems are oriented. The result is exactly 50/50 stem-up and stem-down (3). Just to be certain, we test our apparatus by running the sorted grapes through the same type of stem-direction separator machine a second time (4). The results are that all stem-up grapes are found to be stem-up when re-tested, and all stem-down grapes to be stem-down (5). Our stem-direction separator machine works.

In figure 1.2, we perform the same testing sequence on our color separating device. Beginning with grapes of unknown properties (1), we pass them through a color separator (2), resulting in a split of exactly 50/50 between green and purple grapes (3). Just to be certain, we run the sorted grapes through the same type of machine a second time (4). Again, all green grapes are found to be green when re-tested, and all purple grapes to be purple (5). Our color separator machine works.

2. Testing for Two Properties. Referring to figure 2.1, we will now test the quantum grapes sequentially to learn everything we need to know about them. Beginning with grapes of unknown properties (1), we pass them first through our stem-direction separator (2), resulting in 50/50 stem-up and stem-down grapes (3). We pass them next through our color separator (4), resulting in a 50/50 split between green and purple grapes (5).

So far, so good. If these were garden-variety grapes, we would now know both the stem direction and the color of the four batches of grapes at (5), because we learned the stem direction at steps (2-3), and the color at steps (4-5) of figure 2.1. We could bring the top-most bunch of grapes in the diagram to the boss, because they have been tested for stem direction and found to be 100% stem up; and they have been tested for color and found to be 100% green. What is more, we know from our testing that green grapes stay green grapes, and stem-up grapes stay stem-up grapes. (Don't we?)

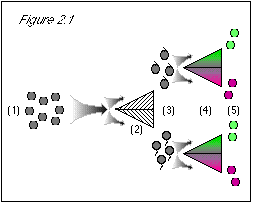
But these are quantum grapes, and the boss was very specific that we must be absolutely certain of our results. Even though we know that both of our separator machines work perfectly, we also know that the boss will not take our word for the properties of the gray blobs we place in front of her, but will perform her own tests to see if we have done as she demanded. And so . . ..

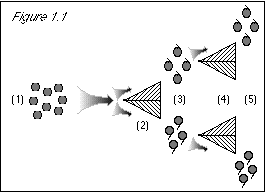
As shown in figure 2.2, and just to be certain, we now re-test the grapes, most recently sorted for color, to confirm their stem direction. We pass the green grapes at step (5) (which should be all stem-up), through the stem-direction separator a second time (6).

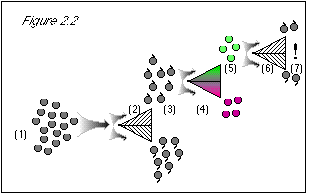
Surprise and consternation! The stem-direction separator now shows two equal groups of grapes, split 50/50 between stem-up and stem-down (7), despite the fact that we've already sorted these grapes for stem direction, so that all of the grapes at step (7) should have been stem-up. What happened to our stem-up quantum grapes between step (3) and step (7)?

These are the experimental results. Our native intelligence and common sense tell us that the quantum grapes at step (7) should all be stem-up, because we never put any stem-down grapes through the machine at step (6). The results couldn't be any more shocking if we had put grapes through the machine and ended up with kangaroos and wrist watches. Where did the stem-down grapes come from? We didn't put them there.

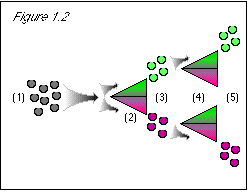
Refining the experiment to test our common sense objections. The only thing that happened to the stem-up grapes we started with at step (3) is that we sorted them for color at steps (4-5). Did the color-sorting process interfere with the stem direction? Perhaps our color separator machine changes the stem direction of every other quantum grape? But how can that be, if the stem direction seems to be an intrinsic property of quantum grapes? (See figure 1.2.)

This is very confusing (and it only gets more confusing). We need to design an experiment to find out what, if anything, the color separator machine does to the grapes' stem directions. Since all we want to know is what happens to a quantum grape's stem direction when it passes through the color separator, we do not need to know anything more about the grape's color. In fact, we would like to cancel out the actual results of the color separator, so that we can test the entire bunch of grapes from beginning to end, focusing only on what happens to the stem direction of stem-up grapes when they pass through a color separator. How can we pass our stem-up quantum grapes through a color separator without actually learning anything about their color?

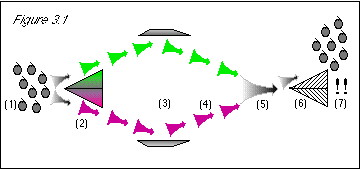
As shown in figure 3.1, we will run a bunch of stem-up grapes (1) through a color separator (2), as we did before. However, we will then bounce the green and purple grapes with deflectors (3), which will send both streams back toward each other (4), and mix them all back together (5). At this point, we will have run the stem-up grapes through a color separator, but we will not know the color of any particular grape going into the stem direction separator (because they will all be mixed up, both green and purple). In effect, we will be only testing a bunch of grapes known to be stem-up, to see if their stem direction has changed as a result of their passage through the color separating machine.

When we perform this "equipment test," we find that the grapes known to be 100% stem-up have remained 100% stem-up (7), despite having gone through the color separator! Apparently, the color separator machine itself does not change the stem direction. Okay, then what changed the stem direction in figure 3.2, steps (3-5), if not the color separator machine?

As a final check on our equipment, what do you suppose would happen if we blocked off the lower stream of purple grapes in the last set up? That way, we again will be testing only the green grapes (thought to be all stem-up) for stem direction. Will we get the result of figure 2.2? Or the result of figure 3.1? (And why should the results be any different?)

Referring to figure 3.2, we block the lower stream of purple quantum grapes at (4), so that they do not rejoin the stream at (5).

When we do this, the stem-direction separator (6) shows 50/50 stem-up and stem-down (7), as in figure 2.2. (Note that the output is down by half, indicating that we got what we wanted at step (5), which is the top stream of green grapes only.)

At wit's end. After all of our careful manipulations, we still haven't come up with a pile of quantum grapes about which we can be certain of both the color and the stem direction. We still have nothing to show the boss. And we can't think of any more or different tests that will give us a pile of grapes where we are certain of both the color and the stem direction. There is something wrong with these quantum grapes.

We sit by our final equipment set up, heads cast down. We have left it running, so that a steady stream of stem-up grapes are bouncing into the color separator, heading up and down, bouncing off the deflectors and back toward the mixing point. The blocking wall at (4) is in place, and the grapes popping out of the stem-direction separator are 50/50 stem-up and stem-down. Idly, we pull the blocking wall back and let the two streams mix. Immediately, grapes stop popping out of the bottom of the stem-direction separator, but pop out of the top much faster, piling up into the stem-up pile. We push the blocking wall back in place, and the green grapes going into the stem direction separator resume a slower divided flow, and again pile up in two stacks at (7): stem-up at the top, and stem-down at the bottom. Pull the wall out - the stream heads upward; push the wall in - the stream divides; pull the wall out . . ..
Our minds wander back to the previous chapter, when we were sitting by a double slit experiment, idly playing with the electron detectors at the slits, turning them off, then on, then off, then on; watching the pattern at the rear wall change from interference pattern, to clumping pattern, to interference pattern, to clumping pattern . . ..
What is going on with these quantum grapes?

It seems that the same quantum grape can be either stem-up or stem-down. Maybe we should say that a quantum grape is both stem-up and stem-down, but we only see one aspect at a time, just like we can say that a coin is both heads and tails, but we only see one side at a time - except that sometimes the quantum grape acts like it does have just one stem direction, like a coin that always comes up heads. Or maybe we should say that a quantum grape doesn't really have any stem direction at all - except that when we look for a stem direction, we see a stem direction; and our seeing a stem direction will have an effect on how the grape behaves in the separating machines. And our seeing a color will have an effect on how the grape behaves in the separating machines. Our seeing a color will have an effect on the stem direction. And what is this effect?

There is something intriguing about this 50/50 result that we get (1) whenever we do not know the property for which we are testing, and (2) whenever we know the other property. What does a 50/50 result mean? Does it mean, for example, that the grapes will come out in alternating colors - green, purple, green, purple, green, purple, . . . etc.? The answer is no. When we look carefully at the grapes coming out of the separator machines, we find that a 50/50 result means only that the eventual, overall result will be 50/50; there is no pattern in the color or stem direction of the grapes coming out of the machines in these situations. We might as well flip a coin as try to guess which way the next quantum grape will come out of the machine. And, just like flipping coins, it is only the overall result that comes out 50/50. (This is similar to the way patterns built up in the double slit experiments, if you recall - unpredictable for individual results, but according to a statistical pattern for the overall result.) In the case of the quantum grapes, the 50/50 result is the same as saying that the property is random.

We have never before encountered properties that seem to be fixed or intrinsic if we know the property, but random if we do not know the property and random if we know another related or complementary property. With quantum grapes, it appears that a completed measurement of one property (i.e., an observation that is noted, or a testing accompanied by obtaining the results) has an effect on the quantum grape itself in two respects: first, measuring property A yields a result, and now we can say that the quantum grape has a property A, and that the quantum grape's "A property" is such and such. Second, the same completed measurement of property A leads to a specific result in the next measurement of complementary property B, and that result is that property B will be random upon its next measurement, no matter what. This is a remarkable "measurement effect," which leads to a fundamental problem in our ability to be certain at any given point in time about both property A and property B: by being 100% certain of property A, we are 100% uncertain about property B. What is more, our uncertainty about property B appears to be for no other reason than that we are certain about property A.

[Note to the reader: Do not be concerned that you may feel you do not understand exactly what is going on in physical terms. As the physicist Richard Feynman frequently observed, nobody understands exactly what is going on in physical terms. And Richard Feynman was generally acknowledged to be a genius.]

Searching for an explanation. Now . . . what are we going to tell the boss? I imagine the conversation going something like this:

        Us: Boss, we are unable to fulfill your request for quantum grapes that are both certainly green and certainly stem-up.

Boss: Fine. You're fired, and I'll find somebody who can.

        Us: There is no such person. The request cannot be fulfilled.

Boss: What do you mean by that?

    Us: It appears to be the nature of quantum grapes that if you know the color, you cannot know the stem direction, and vice versa.

Boss: Well, there must be something wrong with your equipment. Get better equipment.

    Us: There does not appear to be anything wrong with our equipment. It appears that the very fact that we are certain about the color destroys our certainty about the stem direction; and the very fact that we are certain about the stem direction destroys our certainty about the color.
To put it another way, it appears that quantum grapes can either have a color, or they can have a stem direction: they cannot have both at the same time. When we test quantum grapes for color, they have a color which is either green or purple; at that time, they do not have a stem direction. Likewise, when we test quantum grapes for stem direction, they have a stem direction which is either stem-up or stem-down; at that time, they do not have a color. Whenever we test a quantum grape which does not have a color and measure its color, it will always have a 50/50 chance of being green or purple, completely at random, like flipping a coin. Likewise, whenever we test a quantum grape which does not have a stem direction and measure its stem direction, it will always have a 50/50 chance of being stem-up or stem-down.

Boss: What nonsense is this?

    Us: It is as though [and here we take a deep breath and bite our lip] . . . it is as though the quantum grape truly has neither color nor stem direction, but when we test for these properties - then the quantum grape obligingly produces a color or stem direction for our benefit. The color or stem direction thus produced is semi-permanent, in the sense that the quantum grape will continue to exhibit this property unless and until we test for the other property and actually learn the results of that test. At that point, the previously measured property disappears, and the newly demanded property obligingly appears as though it had never previously existed and must be - how shall we say this - must be recalculated according to the 50/50 formula.

Boss: Do you mean to tell me that these quantum grapes are intelligent? That they know what we know and tailor their properties according to the state of our knowledge?

    Us: Well, not exactly. All we mean to say is that their properties appear to exist for the sole purpose of satisfying our curiosity about their properties; but that, for the two related properties of color and stem direction, they can satisfy only one such curiosity at a time. When we look for a grape's color, it is assigned a color, and from that point on, it has a color - unless we look for the same grape's stem direction, in which case it will be assigned a stem direction. Something about the process of assigning the stem direction seems to erase the color assignment, so that the next time we look for the grape's color, the color has to be assigned anew.

Boss: [Who knows something about computer programming.] It sounds like you're trying to describe a memory variable in a computer program, which holds firsts one value and then another. In this case, the color and stem direction properties are assigned to the same memory variable, so that only one can exist for any given calculation. If the memory variable holds, say, the color property, and if the stem-direction property then is called for, the program would need to generate a new stem-direction property and place it at that memory location. Of course, that would immediately displace the color property, so that the same cycle would be repeated the next time the color property is called for.

    Us: Yes. Your computer programming analogy is good. Oddly enough, we find it most helpful to think of the quantum grapes not as actual, solid grapes, but as images of grapes produced according to a formula. At least as far as a visual inspection of their color and stem direction is concerned. Frankly, we don't know what would happen if we tried to use our sense of taste to assess their juiciness properties, or our sense of touch to test their weight properties. The New York Times article didn't mention these. [Aside: And you don't pay us enough to bite into one.]
Notice, by the way, that all of the quantum grapes of a given variety are exactly alike - not at all like real grapes, which always have some distinctive variations. Every green quantum grape is exactly like every other green quantum grape, as though each quantum grape image were being calculated and produced according to a formula. Don't you find this odd? The only "things" we can think of that are all exactly alike are pictures that have been reproduced from a master image, like icons on a computer screen.
At any rate, our hypothesis that the quantum grapes are only images, produced on demand according to a formula, is consistent with our experimental results. The color and stem direction properties of these quantum grapes are nothing like the color and stem direction properties of the grapes served in the company cafeteria.

Boss: So, what is your conclusion?

    Us: With regard to color and stem direction, the quantum grapes follow the quantum mechanical law known as the uncertainty principle. Because of that quantum quirk, you will never be certain of both the color and stem direction of any quantum grape.

Boss: Gotcha.

Surrendering to the math. Now that you, the reader, have wrestled with an attempt to imagine quantum units as if they were like objects in our experience, you may appreciate the elegance of the uncertainty principle, and its power in predicting the result of experiment. First, recall that we are dealing with properties that can be only one way or the other: green or purple; stem-up or stem-down. Second, recall that in such an either/or situation, you can be only (1) 100% certain about the property, or (2) 100% uncertain about the property. You either know the color or you don't; you either know the stem direction or you don't. In such a situation, the uncertainty principle can be stated as follows:

For two complementary either/or properties, the certainty of knowledge of one property will necessarily lead to the complete uncertainty of knowledge of the other property.

Or, to put it even more starkly:

If you know one complementary either/or property, you do not know the other property (regardless of what you thought you knew, or what you actually did know).

The necessary consequence of the uncertainty principle in these either/or situations is that the very act of obtaining knowledge about one complementary property destroys all knowledge of the other property.[3] Since this quantum mechanical law cannot (or, at least, does not) make you forget everything you previously knew about the other property, it must change the property of the quantum unit itself, to make sure that anything you previously knew no longer applies. (Never mind how or why; it just does.) A random 50/50 result represents a total surrender of all knowledge and predictability: the result could come out either way, and you have no way of knowing or predicting which way.

For a moment, just surrender to the logic of quantum mechanics and review the quantum grape experiments in light of the uncertainty principle, which is nothing more and nothing less than a law of nature. Let us review our experiments with "quantum grapes," focusing only on the state of our knowledge at each step of the process.

Figure 1.1: When we first run the grapes through the stem direction separator (2), we know nothing about their color property. The uncertainty principle does not prevent us from knowing their stem direction. But at this point, we know nothing about their stem direction anyway. Based on our previous lack of knowledge of stem direction, the results come out 50/50 for this either/or property (3).
When we next run the grapes through the stem direction separator (4), we know their stem direction, but we still know nothing about their color. The uncertainty principle still does not prevent us from knowing their stem direction. Based on our prior knowledge of the stem direction (and our lack of knowledge about color), the results are consistent with our knowing the stem direction, i.e., the stems remain in the positions we know.

Figure 1.2: Similarly, when we first run the grapes through the color separator (2), we know nothing about their stem direction property. The uncertainty principle does not prevent us from knowing their color. But at this point, we know nothing about their color anyway. Based on our previous lack of knowledge of color, the results come out 50/50 for this either/or property (3).
When we next run the grapes through the color separator (4), we know their color direction, but we still know nothing about their stem direction. The uncertainty principle still does not prevent us from knowing their color. Based on our prior knowledge of the color (and our lack of knowledge of stem direction), the results are consistent with our knowing the color, i.e., the colors remain as we know them.

Figure 2.1: When we first run the grapes through the stem direction separator (2), we know nothing about their color property. The uncertainty principle does not prevent us from knowing their stem direction. Based on our previous lack of knowledge of stem direction, the results come out 50/50 for this either/or property (3).
When we proceed to run the grapes through a color separator (4), we know their stem direction, and the uncertainty principle states that we then do not know their color. (This is not a problem at this point, since we did not expect that we knew their color.) Since we do not know their color, the results come out 50/50 for this either/or property (5).

Figure 2.2: Beginning at step (6), when we run the grapes through the stem direction separator, we know their color. The uncertainty principle states that we then know nothing about their stem direction. Therefore, the result is 50/50 stem-up and stem-down (7).
At this point, we see how the uncertainty principle agrees with experimental results, but conflicts with common sense. Because know the grapes' color at step (6), we do not know their stem direction, despite the fact that we had previously measured their stem direction at steps (2-3). To make the uncertainty principle's statement true, i.e., in order that we do not know the stem direction, we must come up with a 50/50 result at step (7), and the only way to do this is to discard the results at step (3), where we learned the grapes' stem direction. This way, we can start over with a clean slate at step (6), knowing nothing about the grapes' stem direction.

Figure 3.1: When we first run the grapes through the color separator (2), we know their stem direction. The uncertainty principle states that we then know nothing about their color, and so half of the grapes will follow the green path and half of the grapes will follow the purple path.
When we rejoin the two streams (5), we do not actually know anything about the color of the grapes, since they may be either green or purple, in a random 50/50 mix. Therefore, the uncertainty principle does not prevent us from knowing the stem direction.
When we run the mixed grapes through the stem direction separator, since we know the stem direction to be stem-up, the result is that the grapes are stem-up (7).

Figure 3.2: Because we knew the stem direction of the grapes when we ran them through the color separator (off screen, from figure 3.1), half of the grapes followed the green (upper) path, and half followed the purple (lower) path; therefore, by blocking the purple (lower) path, we reduce the output at (7) by half.
When we run the half-stream of grapes through the stem-direction separator (6), we know their color property, in that they will all be green (having all followed the green path through the color separator). The uncertainty principle states that we will then know nothing about their stem direction property. If we know nothing about the stem direction property, the result will be 50/50 stem-up and stem-down at step (7). And so it is. Because we knew the grapes were green, we lost our knowledge of their stem direction.

Simple, isn't it? And what do you think would happen if we ran the quantum grapes at fig. 3.2, step (7) through a color separator? If you guessed that they would turn out 50/50 green and purple, because we know their stem directions, you are right! That's the uncertainty principle. It's a law of nature. And when these experiments are conducted on any quantum unit for any set of complementary, either/or properties, these are the results. If we are 100% certain of one property, we are 100% uncertain of the complementary property.

Uncertainty and the measurement effect. The quantum uncertainty principle embodies the "measurement effect" that we saw in the previous chapter. That is, when we measure one complementary property, our measurement itself has an effect on the other complementary property. In the world of quantum mechanics, it is not at all peculiar to say that the randomization of the quantum grapes' stem directions has been caused by our measurement of the color. In the earlier example of the state trooper, you may now see that we can say with a perfectly straight face that the trooper caused the cars to stretch out along the highway by increasing the accuracy of the measurements he was taking with the radar gun. In the measurement effect we saw in the last chapter, our measurement of the position of the electron at the slits had the effect of causing there to be an electron "particle" at a particular location; this, in turn, caused the wave-like interference pattern to disappear and be replaced by a particle pattern. Recall that the most puzzling, even shocking, aspect of that measurement effect was that a "measurement" turned out to be the point in time when we gained knowledge of the location property of the electron unit, rather than the point when some mechanical device gathered and recorded the data. Recall further that this was true even when we gained (or decided not to gain) the knowledge long after the mechanical measurement was complete in every detail. The difference lay in whether we knew one thing at the time we tried to find out another thing.

This most puzzling aspect of the measurement effect is an integral part of the uncertainty principle. The "certainty" which will affect quantum measurements is the subjective certainty of the researcher, rather than any definite or otherwise certain (in the mechanical sense) distinction made by the laboratory equipment. This is most clearly illustrated by figure 3.1 and figure 3.2 in the "quantum grape" series: the difference in results lay not with any mechanical process involving the quantum grapes, but rather with whether we knew the color of the grapes when we tested them for stem direction. Going back to the state trooper illustration, we can now see that the radar gun itself had no effect on the car; but the trooper's act of reading the radar gun caused the car to stretch out into a blur of possible positions along the highway. The orthodox formulation of the uncertainty principle incorporates this subjective standard of certainty/uncertainty: it is an increase in the certainty of knowledge of one property - not merely an increase in the accuracy of the experimental equipment - that will necessarily lead to a decrease in the certainty of knowledge of the other property.

Rethinking the nature of quantum properties. We found that thinking of the quantum grapes as "things" which had measurable "properties" led us to hopeless confusion in trying to reconcile the experimental results. On the other hand, the uncertainty principle neatly predicts the results in a precise, mathematical way, but offers no suggestion of any model for the underlying processes. Quantum mechanics itself has never produced any satisfactory intellectual explanation of why quantum units behave the way they do, and most scientists have given up trying.[4] To ask of quantum mechanics, "Why do complementary properties relate to each other according to the uncertainty principle?" or, "Why does the measurement effect occur at the point of subjective knowledge?" is about as meaningful as asking, "Why does two plus two equal four?" About the only answer possible is, "Because that's the way the math works." And so the scientific community is left with a mathematical description of quantum processes so rigorous and exact that it is sometimes described as a "perfect theory," yet so lacking in intellectual content that it remains profoundly unsatisfying. Quantum theory is the culmination of centuries of effort directed toward answering the basic questions of nature, yet it recalls nothing so much as the parent's frustrated end-of-the-line answer to the curious child: "Why? You're asking me why? Because, that's why. Just because."[5]

Therefore, we will not be upsetting any scientific applecarts if we try a different approach. Let us follow through on the logic and intuition of our hypothetical employees and their hypothetical boss.

Computer programming as a model of complementary properties. Suppose we think of the "quantum grapes" (which is to say, any quantum units) not as solid, substantive "things," but as images produced by a computer. If they are images produced by a computer, then whatever properties they possess are only the result of some formula used by the computer to generate images. More properly, the images would be the products of a computer "algorithm," which is a step-by-step procedure used by the computer to arrive at a desired result. In common usage, a computer "algorithm" is essentially synonymous with a computer "program," which is the set of rules and instructions that tell the computer what to do and when. What step-by-step procedure could the computer be using to produce its images according to the uncertainty principle?

Suppose that, when the computer needs values for a property, it can assign a temporary value for the purpose of tracking the quantum unit as a "virtual" object (that is, potential information that can be presented to the user if necessary). The computer can continue to deal with the temporary value until the user needs a value.

Suppose further that, from the computer's point of view, the user "needs" a value for the property whenever he or she does anything that would reveal the property. At that point, the computer must make a choice from among the range of values at which the property can be pegged, so that a definite value for the property can be displayed. So the computer assigns a value to that property, generates and displays the image in a form that the user can "read," and stores the properties of the image for future reference.

Suppose further that --

if there is no stored value for a property needed by the user, the computer randomly assigns a value for the property from among the range of possible values (in the either/or case, this range consists of 0 or 1, so the computer only needs to do something like flipping a coin);
in the case of complementary properties A (color) and B (stem direction), the values are stored at the same memory location, which we will call "location A/B";
whenever the computer stores a value for property A, any value previously stored at location A/B (i.e., a value for property B) is erased - replaced by the value for property A;

it follows that the next time the computer checks for a value for property B, there will be none; and since there is no stored value for property B, the computer again will assign a value from among the range of possible values (0 or 1).

This program design will yield the results embodied in the uncertainty principle. Let us see how.

Figure 1.1:
(1) Begin with no stored values for either property.
(2) The computer needs a value for the stem direction property so that it can divvy up the quantum grapes into two streams according to stem direction. It checks memory location A/B and finds no stored value for stem direction; so it arbitrarily assigns a temporary stem direction from the range of possible values (0 or 1), which it uses for divvying up the quantum grapes into streams. In order to maintain an overall 50/50 ratio, but to save itself the trouble of remembering what value it last used (i.e., to save on memory), the computer employs a random assignment process, like flipping a coin.
(3) The user needs a stem direction value to check the results of the stem direction separator; so the stem direction value temporarily assigned at (2) is stored at memory location A/B, and the computer generates an image with that value.
(4) The computer needs a value for the stem direction property so that it can divvy up the quantum grapes according to stem direction; it checks location A/B and finds the stored value, which it uses for divvying up the stream of quantum grapes.
(5) The user needs a value for the stem direction property; the computer checks location A/B, finds the stored value, and generates another image with that value.

Figure 1.2:
The same process is followed for the color property.

Figure 2.1:
(1) Begin with no stored values for either property.
(2) The computer needs a value for the stem direction property so that it can divvy up the quantum grapes into two streams according to stem direction; it checks memory location A/B and finds no stored value for stem direction; so it arbitrarily assigns a temporary stem direction from the range of possible values, which it uses for divvying up the quantum grapes into streams.
(3) The user needs a stem direction value to check the results of the stem direction separator; so the stem direction value temporarily assigned at (2) is stored at memory location A/B, and the computer generates an image with that value.
(4) The computer needs a value for the color property so that it can divvy up the quantum grapes into two streams according to color; it checks location A/B and finds no stored value for color; so it assigns a temporary color value, which it uses for divvying up the quantum grapes into streams.
(5) The user needs a value for the color property to check the results of the color separator; so the color value temporarily assigned at (4) is stored at memory location A/B (displacing the stem direction value), and the computer generates an image with that value.

Figure 2.2:
(1), (2), (3), (4), and (5) The same process is followed as in figure 2.1.

(6) The computer needs a value for the stem direction property so that it can divvy up the quantum grapes into two streams according to stem direction; it checks memory location A/B and finds no stored value for stem direction (the stem direction value having been displaced by the color value at step (5)); so it arbitrarily assigns a temporary stem direction from the range of possible values, which it uses for divvying up the quantum grapes into streams.
(7) The user needs a stem direction value to check the results of the stem direction separator; so the stem direction value temporarily assigned at (6) is stored at memory location A/B, and the computer generates an image with that value.

Figure 3.1:
(1) Begin with quantum grapes which have a stem direction value both assigned and stored at location A/B.
(2) The computer needs a value for the color property so that it can divvy up the quantum grapes into two streams according to color; it checks location A/B and finds no stored value for color; so it assigns a temporary color value, which it uses for divvying up the quantum grapes into streams.
(3), (4), (5) The computer does not need to do anything in terms of values for either property.
(6) The computer needs a value for the stem direction property so that it can divvy up the quantum grapes into two streams according to stem direction; it checks location A/B and finds the stored value for stem direction, which it uses for divvying up the stream of quantum grapes. The original stem direction value was never displaced at location A/B because the user never needed the color value, and so no color image was ever generated, and the temporary color value assigned at step (2) was never stored.
(7) The user needs a value for the stem direction property to check the results of the stem direction separator; the computer checks location A/B, finds the stored value, and generates an image with that value.

Figure 3.2.
(1), (2), and (3) [offstage] The same process is followed as in figure 3.1.
(4), (5) By blocking off the stream of purple grapes, the user has done something that will reveal the color property. That is, all the grapes blocked at (4) will be purple, so that all the grapes arriving at (5) will be green. The computer interprets this as the user needing a value for the color property, so the color value temporarily assigned at (2) is stored at memory location A/B (displacing the stem direction value), and the computer generates an image with that value.
(6) The computer needs a value for the stem direction property so that it can divvy up the quantum grapes into two streams according to stem direction; it checks location A/B and finds no stored value for stem direction (the stem direction value having been displaced by the color value at steps (4-5)); so it arbitrarily assigns a temporary stem direction from the range of possible values, which it uses for divvying up the quantum grapes into streams.
(7) The user needs a value for the stem direction property to check the results of the stem direction separator; the computer checks location A/B and finds no stored stem direction value (having been displaced by the color value); so the stem direction value temporarily assigned at (2) is stored at memory location A/B, and the computer generates an image with that value.

So it works to use simple computer processes as a model for these quantum behaviors. It's simple, and it's easy on the brain. It works just as well as the uncertainty principle in predicting results, and it doesn't present any insurmountable problems of relating itself to human experience. We use two old tricks of computer programming - the temporary value of a variable, and the stored value of two variables which share a single memory location - which were developed back in the early days when processors were slow and memory was expensive and so programming had to be efficient. We can easily conceive of a computer program which would generate these results using these programming tricks, or something very like them. [6]

Both the shared memory arrangement and the random assignment system allow the computer to satisfy the user's information requirements with a minimum set of rules (programming) and memory usage. By storing a single master image formula for the quantum unit, the computer can generate billions and trillions and untold quadrillions of such images with no more fuss than generating one image, and simply plug the variable values into each image as necessary. These efficiencies would recommend themselves in a program designed to simulate an entire universe.

Moreover, the measurement effect's relationship to the subjective knowledge of the experimenter is neatly addressed by this metaphor, because the entire set up is nothing more than a "user interface," i.e., a way to convey to the user the information held by the computer. A computer's function, its very purpose, is to process information for presentation to the user, and so the display of information to the user is the event on which the computer's operations hinge.

In the absence of any other intellectual model to use as a guide to imagining what may be causing these effects, it may be that we can use this computer model in other areas of quantum mechanics. Such a mental image will be useful if it can help us to bring some order to our thinking about these matters. If computer programming and display prove to be good models for other quantum mechanical behaviors that are incomprehensible in terms of the behavior of "things," then we may examine the model more closely. Ultimately, we would come back around to the why - why do the component parts of the universe behave in ways that closely resemble computer processes?

Chap. 3 Uncertainty

Endnotes

1 [Back]	Mathematically, this relationship is as follows: the uncertainty (D) in momentum (X), multiplied by the uncertainty in position (P), must be greater than or equal to Planck's constant (h-bar). Planck's constant of action is an incredibly small but very definite number. The usual Heisenberg uncertainty relation for position and momentum is expressed as: DXDP >= h-bar/2 Recently, it has been suggested that this indefinite formulation (greater than or equal to) may be replaced by an exact equality: dXDP_nc = h-bar/2 New Scientist article: http://www.newscientist.com/news/news.jsp?id=ns99992209 LANL archive paper: M.J.W. Hall and M. Reginatto, "Quantum mechanics from a Heisenberg-type equality," http://xxx.lanl.gov/PS_cache/quant-ph/pdf/0201/0201084.pdf
2 [Back]	This fanciful narrative presents the combined results of a number of different experiments carried out over many years, conducted with electrons, photons or other quantum units; and the thought experiments of John Wheeler. Because all quantum units exhibit the behaviors described here, we can consider these laboratory results as constituting one long series of experiments with one quantum unit (quantum grapes), which makes for a cleaner and easier presentation. I am particularly indebted to David Albert's discussion and diagrams from Quantum Mechanics and Experience, and in the May 1996 issue of Scientific American.
3 [Back]	For properties which can vary over a wider range, such as position and momentum, the statement would refer to obtaining complete knowledge about one complementary property.
4 [Back]	Stephen Hawking observes that, "In effect, we have redefined the task of science to be the discovery of laws that will enable us to predict events up to the limits set by the uncertainty principle." (A Brief History of Time at 173.)
5 [Back]	In this remark, I am not referring to the most obvious way in which quantum theory is "incomplete," which is its lack of any description for the mechanics of gravity (which we have not discussed yet). Much of the present-day effort in theoretical physics is directed towards finding a way to describe gravity in the same terms as, say, electrons and photons. Although there is some loose talk that, by accomplishing such a "grand unification theory," science will have explained "everything," we can see that quantum theory itself explains nothing. Quantum theory only describes (quite accurately) the inexplicable.
6 [Back]	The experimental basis for the parable of the grapes, and the metaphor of the eraseable bit of memory, were recently described in a profile of Anton Zeilinger in The New Scientist, 17 February 2001. (Anton Zeilinger has performed some of the most exacting tests of quantum nonlocality, as described in Chapter 7.) "In quantum mechanics, these building blocks [of the material world] are called elementary systems, and the archetypal elementary system is the spin of an electron. The only possible outcomes of measuring an electron's spin are "up" and "down". You can choose any axis to measure the spin along--vertical, horizontal or tilted--but once that axis is chosen, only the two results are possible, as if the electron were a spinning top that can be one way up or the other, but can't point to any intermediate direction. These outcomes could just as well be labelled "yes" and "no", or, in the fashion of digital computers, "1" and "0". "Zeilinger's principle leads to the intrinsic randomness found in the quantum world. Consider the spin of an electron. Say it is measured along a vertical axis (call it the z axis) and found to be pointing up. Because one bit of information has been used to make that statement, no more information can be carried by the electron's spin. Consequently, no information is available to predict the amounts of spin in the two horizontal directions (x and y axes), so they are of necessity entirely random. If you then measure the spin in one of these directions, there is an equal chance of its pointing right or left, forward or back. This fundamental randomness is what we call Heisenberg's uncertainty principle." See also A. Zeilinger, "On the Interpretation and Philosophical Foundation of Quantum Mechanics"

The Reality Program

by Ross Rhodes

9/15/02

The Notebook of Philosophy & Physics

Its existence property is:	existing (as opposed to all the billiard balls the manufacturer plans to make next year)
Its shape property is:	spherical
Its weight property is:	6 ounces
Its color property is:	black
Its number property is:	8
Its number orientation property is:	at the top
Its spin property is:	spinning
Its spin direction property is:	clockwise
Its location property is:	on the table
Its temperature property is:	about room temperature
Its motion-with-respect-to-the-table property is:	standing still (but spinning)

Us:	Boss, we are unable to fulfill your request for quantum grapes that are both certainly green and certainly stem-up.
Boss:	Fine. You're fired, and I'll find somebody who can.
Us:	There is no such person. The request cannot be fulfilled.
Boss:	What do you mean by that?
Us:	It appears to be the nature of quantum grapes that if you know the color, you cannot know the stem direction, and vice versa.
Boss:	Well, there must be something wrong with your equipment. Get better equipment.
Us:	There does not appear to be anything wrong with our equipment. It appears that the very fact that we are certain about the color destroys our certainty about the stem direction; and the very fact that we are certain about the stem direction destroys our certainty about the color. To put it another way, it appears that quantum grapes can either have a color, or they can have a stem direction: they cannot have both at the same time. When we test quantum grapes for color, they have a color which is either green or purple; at that time, they do not have a stem direction. Likewise, when we test quantum grapes for stem direction, they have a stem direction which is either stem-up or stem-down; at that time, they do not have a color. Whenever we test a quantum grape which does not have a color and measure its color, it will always have a 50/50 chance of being green or purple, completely at random, like flipping a coin. Likewise, whenever we test a quantum grape which does not have a stem direction and measure its stem direction, it will always have a 50/50 chance of being stem-up or stem-down.
Boss:	What nonsense is this?
Us:	It is as though [and here we take a deep breath and bite our lip] . . . it is as though the quantum grape truly has neither color nor stem direction, but when we test for these properties - then the quantum grape obligingly produces a color or stem direction for our benefit. The color or stem direction thus produced is semi-permanent, in the sense that the quantum grape will continue to exhibit this property unless and until we test for the other property and actually learn the results of that test. At that point, the previously measured property disappears, and the newly demanded property obligingly appears as though it had never previously existed and must be - how shall we say this - must be recalculated according to the 50/50 formula.
Boss:	Do you mean to tell me that these quantum grapes are intelligent? That they know what we know and tailor their properties according to the state of our knowledge?
Us:	Well, not exactly. All we mean to say is that their properties appear to exist for the sole purpose of satisfying our curiosity about their properties; but that, for the two related properties of color and stem direction, they can satisfy only one such curiosity at a time. When we look for a grape's color, it is assigned a color, and from that point on, it has a color - unless we look for the same grape's stem direction, in which case it will be assigned a stem direction. Something about the process of assigning the stem direction seems to erase the color assignment, so that the next time we look for the grape's color, the color has to be assigned anew.
Boss:	[Who knows something about computer programming.] It sounds like you're trying to describe a memory variable in a computer program, which holds firsts one value and then another. In this case, the color and stem direction properties are assigned to the same memory variable, so that only one can exist for any given calculation. If the memory variable holds, say, the color property, and if the stem-direction property then is called for, the program would need to generate a new stem-direction property and place it at that memory location. Of course, that would immediately displace the color property, so that the same cycle would be repeated the next time the color property is called for.
Us:	Yes. Your computer programming analogy is good. Oddly enough, we find it most helpful to think of the quantum grapes not as actual, solid grapes, but as images of grapes produced according to a formula. At least as far as a visual inspection of their color and stem direction is concerned. Frankly, we don't know what would happen if we tried to use our sense of taste to assess their juiciness properties, or our sense of touch to test their weight properties. The New York Times article didn't mention these. [Aside: And you don't pay us enough to bite into one.] Notice, by the way, that all of the quantum grapes of a given variety are exactly alike - not at all like real grapes, which always have some distinctive variations. Every green quantum grape is exactly like every other green quantum grape, as though each quantum grape image were being calculated and produced according to a formula. Don't you find this odd? The only "things" we can think of that are all exactly alike are pictures that have been reproduced from a master image, like icons on a computer screen. At any rate, our hypothesis that the quantum grapes are only images, produced on demand according to a formula, is consistent with our experimental results. The color and stem direction properties of these quantum grapes are nothing like the color and stem direction properties of the grapes served in the company cafeteria.
Boss:	So, what is your conclusion?
Us:	With regard to color and stem direction, the quantum grapes follow the quantum mechanical law known as the uncertainty principle. Because of that quantum quirk, you will never be certain of both the color and stem direction of any quantum grape.
Boss:	Gotcha.