Computer Waves, Computer Particles, and Computer Properties
In the case of digital sound, the computer's memory
stores a series of numbers representing the height and depth of the "wave" described by a
microphone magnet moving back and forth in space, and forward in time. This stored
representation of the microphone wave is used to move the loudspeaker magnet, tracing the same
"wave." Using the y = sin(x) + sin(2.5x) wave that we know from chapter 1 (representing the
combination of two simple tuning forks), we saw how this measuring process works.
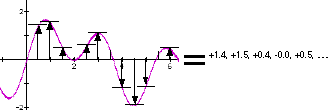
By "sampling" (i.e., measuring) the graphic wave every 0.5 units along the horizontal line (the x
axis, representing time), we have turned the graph into a string of numbers. These numbers are
stored in the computer's memory. When we reverse the process, to turn the string of numbers into
a graphic wave, we have to do some approximation. That is, in the above example, the recreated
wave will not look exactly like the wave we "sampled," because we only measured every so often.
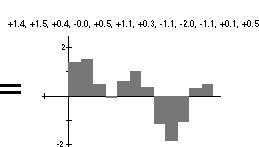
In fact, the computer on which I composed this text and illustrations was able to generate my graphic wave illustration using nothing more than a very simple formula -- y = sin(x) + sin(2.5x) -- representing two perfect tuning forks. I could have used a pencil to draw a wave by hand, and then "scanned" it with a machine which would turn it into a computer graphic; but I did not. It was easier to have the computer calculate and draw a curve from the formula. (In fact, the computer did a much better job than I could have done with a pencil.) And so, with my wave illustrations, there is no "original," in the sense that there is no piece of paper, no freehand illustration that the computer is reproducing or approximating. The "original" is just a string of numbers created and stored by my computer, and in my computer, at my direction. In terms of sampling, I would have to stop somewhere between 72 and 600 measurements per inch (depending on what I am drawing), which are the effective resolution limits imposed by my computer memory, my graphics software, and my printer. If I measured 600 times per inch, I would have one measurement for every step of the "original" picture. At that point, I would have an exact replica of the "original" graphic of the wave, which itself was created stepwise. Further sampling would not increase the detail, because there is no more detail to be had in the "original."
The computer could just as easily generate a wave pattern
for a more complex sound, that is, for an instrument a bit more sophisticated than two tuning
forks. That is exactly what happens in a musical synthesizer, and you have heard the results on
thousands of music recordings which use synthesizers. If you have a recent vintage computer at
home or at work, it probably has a "sound card" installed, which is just such a sound synthesizer.
Pretty good sound creation, if you're not a total traditionalist.[2]
Since the computer is simply calculating a shape to
represent what the desired sound wave would look like if it were to be played, there is no need to
actually play it, strictly speaking. In fact, it is entirely possible for the computer to calculate the
wave, record the wave as a string of numbers, place the numbers into memory (internally, or in the
form of a CD), and place these numbers on your living room shelf in the form of a fully-packaged
CD, without once ever actually playing any music. You can then place the CD in your stereo's
CD-player and set it spinning. At that point, it is entirely up to you whether or not you turn on the
stereo's loudspeakers. (Although I cannot think of a good reason deliberately to play a CD with
the sound turned off, you could do that if you wanted to.) And then you would have a grand
process of computer-created numbers representing anything from good country music to a
symphony orchestra, and the (still hypothetical) music has existed, from beginning to end, as
nothing more or less than a series of numbers. In this scenario, nothing -- no medium -- has ever
"waved."
Imagine the following set up. A musician in a recording
studio plays a synthesizer, controlled by a keyboard. It is a digital synthesizer which uses an
algorithm (programming) to create nothing more than a series of numbers representing what the
desired sound wave would look like. The synthesizer's output is routed to a computer and stored
as a series of numbers. The numbers are burned into a disk as a series of pits that can be read by a
laser -- in other words, a CD recording. The CD is shipped to a store. You buy the CD, bring it
home, and put it in your home entertainment system. The "music" has traveled from the recording
studio to your living room. Through what medium did the music wave travel? To a degree, you
might say that it traveled as electricity through the wires from the keyboard to the computer. But
you might just as well say it traveled by truck along the highway to the store. In fact, this "sound
wave" never existed as anything more than a digital representation of a hypothetical sound wave
which itself never existed. Therefore, although it will produce wave-like effects when placed in
your stereo, this wave never needed any medium other than the computer memory to spread itself
all over the music loving world.
How to create an interference pattern that seems very complex but is
actually quite simple. In our review of interference patterns in chapter 1, we confined
ourselves to the simple and pleasing results of overlapping two symmetrical radiating waves,
because that is the type of interference pattern we were going to be seeing in the double slit
experiments. The two simple sine waves that we combined for our sound wave illustration create a
much more complex resulting wave pattern, despite the fact that each is completely regular and
constructed according to the same formula. (The difference between those two sine waves is only
a matter of scale, with one wave being 2-1/2 times the frequency of the other, and yet the resulting
wave looks relatively complicated.) If we were to combine all of the sound waves generated by a
symphony orchestra, the resulting wave would look quite complicated. (You can examine a vinyl
phonograph record with a magnifying glass or microscope and see the literal representation of such
a wave scratched into the surface of the vinyl.) Despite its apparent complexity, the wave can be
analyzed mathematically and shown to be a composite of each of the various waves that were
produced by the instruments playing at that time. The mathematical procedure for analyzing a
complex wave, to break it down into its component waves, was developed by a French physicist,
Baron J.B.J. Fourier, and is called a Fourier analysis. It is quite well understood, and computers
are very good at it.
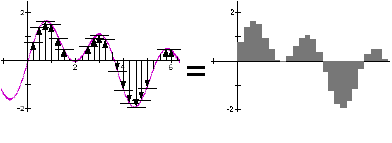
We do not need a lot of instruments to get a complex
pattern. When only two different, i.e., non-symmetrical, wave patterns are overlapped, the
resulting interference pattern quickly breaks down into what looks like chaos, like this:


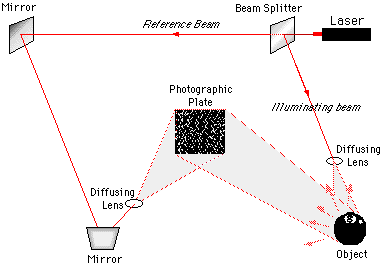
To generate a hologram, we begin with a single laser. We shine the laser at an angled mirror which is semi-transparent, thereby allowing half the light to go through while reflecting the other half of the light. (It works just like the "one-way mirrors" used in police line-ups and department store security set-ups. It looks like a mirror, but some of the light is going through while the rest of the light is being reflected. If you stand on one side, you see a reflection of yourself fixing your tie because you are in a brightly lit room and you only notice the half of the light that is reflected back at you. If you stand on the other side, you see the customer fixing his tie because you are in a darkened room and you only notice the half of the light that is coming through.) This semi-transparent mirror is called a "beam splitter," naturally, because it splits the one laser beam into two laser beams heading in different directions.
In a laser hologram apparatus, one of the two resulting laser beams (it doesn't matter which, because they're both exactly half of the original beam and, therefore, exactly alike) is used to illuminate an object -- say, a billiard ball. That light is reflected by the billiard ball. Using this reflected light from the billiard ball, we use a camera to take a picture of the billiard ball
The trick of laser holography lies in what we do with the other half of the split laser beam, and that is -- nothing. This unmodified half of the split laser beam is called the "reference beam," and it continues on its merry way until it is bounced into the same camera that is taking a picture of the billiard ball. In this way, we have a double exposure -- two beams of light entering the camera at the same time. The first beam is the illuminating beam, which has been reflected off the billiard ball. The second beam is the reference beam, which is essentially unchanged from the time it left the laser.
A laser's great claim to fame is that it produces an extremely regular beam of light. Accordingly, the reference beam is a very regular beam of light shining onto the camera's film. The illuminating beam, on the other hand, has been distorted by having been reflected off the billiard ball by the time it shines onto the camera's film. When the two beams meet on the camera's film, they form an interference pattern. This is just like what happened in the double slit experiment, where our single beam of light was "split" by the two slits and ended up interfering with itself at the back screen. However, in the laser hologram, the two beams are not symmetrical. And what do you think the pattern on the film will look like when the exposure consists of a regular beam of light, on which is superimposed a distorted version of itself? Well, of course, it looks like complete chaos, just like the simple illustration we used earlier.
This is the set-up of a laser hologram in the making:
The final step of laser holography consists simply of
reversing the process. That is, we shine an unmodified laser beam through the developed film.
Because laser beams are so regular, we can use what is essentially an exact copy of the reference
beam when we do this. When the reference beam is shone though the developed film, an image of
the billiard ball appears in the same position (relative to the film) as when it was photographed.
And it appears just as three-dimensional as when we took the picture.
In these modern times, we don't really need billiard balls or laser light. I
have explained laser holograms at some length because the process is not quite as obvious as a
music synthesizer. Nevertheless, the point I want to make is exactly the same as I made with the
example of synthesized sound. Just as computers are very good at generating nice regular sine
wave patterns, they can also produce complex wave patterns with simple instructions. And, of
course, it is no trick for the computer to combine two wave patterns and calculate their
"interference," as we saw earlier.
Now, what would happen if we asked the computer to
generate a nice regular wave pattern to serve as a reference; and to generate a relatively complex
wave pattern, such as might result from light reflected off a billiard ball; and then to combine the
two? Well, we would get a laser-like hologram of a billiard ball, generated entirely by computer.
And, in fact, this can be done. "A computer can be used to calculate the interference pattern
between 2 light beams. By capitalizing on this fact, a hologram can be generated entirely
artificially. An object can be recorded in a hologram without the object ever having existed."[3]
Here is such an image, generated by the Italian National Institute of Optics in Florence, Italy.[4]
It represents the computer's calculations of what light would look like if reflected off a shiny
cone-like surface.

And the computer couldn't care less whether it displays the image or not. For that matter, the computer would be just as happy to produce this complex wave interference pattern in a different medium -- say, the air. In that case, it would be producing sound, using the hologram image as its pattern for the sound wave. Almost certainly, this would be strange to our ears, but similar concepts are being used in technology to help the visually impaired. That is, if a person cannot see but can hear very well, a computer can translate images into sound. This can be quite useful to an unsighted person. A video camera is hooked into a computer, which converts the visual images into digits, and then "plays" the digital picture as if it were a digital sound. These sounds -- however strange -- are played into headphones, so that the unsighted person can "hear" the approach of a lamp post, or curb, or door, much the way a bat creates an image of the physical world by using its hearing to locate objects, and so to navigate around them.
In the same way, the computer can "sculpt" the visual image into an object. That is, the computer can produce this complex wave interference pattern in the medium of papier-mâché or other formable material. For a number of years, computer assisted design ("CAD") programs have allowed architects automatically to use their building plans, drawn on a two-dimensional computer screen, to control lasers which "sculpt" a scale model of the building in cardboard. The same technology allows a computer to "sculpt" the cone-like hologram shown on page 10 of this chapter.
The important points to remember from this illustration of computer holography (as with the illustration of computer sound) are:
(1) The wave has never traveled in any medium in the sense that we are familiar with waves traveling in a medium. It has existed from beginning to end as a string of numbers in the computer's memory.
(2) The computer can handle the entire process from beginning to end without the need for any solid object to be photographed. Such a string of numbers representing a hypothetical wave can create the appearance of an object, and yet this appearance is not a "representation" of any object at all. Truly, the numbers are more real than the object. The image eventually displayed to the user (on demand) is only a visual representation of the information in the computer.The first and only time the information in the computer becomes "real" is when the user demands to see (or hear, or touch) the information in a format that will be meaningful to the user. At that point, we may legitimately ask ourselves which is more "real": the computer generated image (or sound, or model) that we demanded to inspect, or the information in the computer itself?
Recall that the holographic image is basically a combination of just two wave patterns: the reference beam and the illuminating beam. All of the complex distortions of the illuminating beam, caused by the light reflecting off the billiard ball, shake out to a single complicated wave pattern which is distorted in all of those complex ways (just as the orchestra's many component sounds shake out to a single complex wave pattern which can be etched on a vinyl phonograph record and used to move the loudspeaker). Because the hologram records the interference of just these two wave patterns -- the unchanged reference wave and the distorted illumination wave -- the resulting two-wave interference pattern will form the basis of all of the hologram, and also of each and every part of the hologram. Consequently, in every piece of the hologram, you still have the whole interference pattern.
The amount of information that can be extracted from a
smaller section of the hologram is less, which is analogous to a lower sampling rate, or measuring
rate, of our synthesized music sound wave. With music or other sound, a lower sampling rate will
produce a rougher, more approximate version of the original music sound wave. Music sampled at
a rate below about 30,000 times per second sounds relatively hollow and tinny, because it does not
have the detail of the original wave. In the same way, a smaller area of the holographic
interference pattern will produce a lower resolution version of the original image. Holograms
produced from smaller and smaller sections of the holographic plate become increasingly fuzzy.
But, they still show the whole picture. This remarkable quality of the hologram will be interesting
to contemplate when we try to imagine how we might distribute an entire universe worth of
information.

The computer monitor is a simple example of how a computer constructs the most complex graphics (pictures) from the lowly pixel. Computer monitors are the sons and daughters of television sets. They work by sending an electron beam from the back of the picture tube, until it strikes the flat (more or less) front of the tube. The front of the picture tube is coated with a fluorescent material which glows briefly when the electron beam strikes it. By carefully focusing the electron beam, only a single, very small dot appears on the screen. This small dot is the pixel.
The resolution of the picture at the screen -- that is, how
sharp a picture will appear -- is determined primarily by how many dots make up the picture. The
more dots, the sharper the picture, and you can see this by comparing a newspaper photo to a
glossy magazine photo. Assuming that both pictures are in black and white, the main difference is
in how many dots per inch make up the picture. To give you an idea of how many dots make up a
picture, let's take a look at my home computer monitor. My monitor is set for the low end of the
current standard range of resolutions, which is 640 x 480 dots. That is, whatever appears on the moniter is made up of a grid of pixels 640 dots wide and 480 dots high. That means that the
total picture area of the monitor is made up of 307,200 pixels in all. Although this seems like a very large number, I can still
look closely at the monitor and see all the little dots on the screen.
The pixels that make up any computer graphic can be a metaphor for the "particles" that make up the world around us. Consider these characteristics of the pixel:
There are just three kinds of pixels: red, green, and blue. All color graphics are only large collections of various combinations of these three types of pixel.[6] In the same way, we say that all "things" in our world are made up of a limited number of "particles," such as electrons, protons and neutrons.
- Every red pixel is exactly like every other red pixel, and the same is true of blue and green pixels. In the same way, every electron is exactly like every other electron, and the same is true of every proton and every neutron, and every other quantum unit. (The remarkable sameness of every quantum unit has been mentioned briefly earlier in this book, and will be discussed in greater detail later.)
The vast and seemingly limitless variety of computer graphics -- ranging from letters of the alphabet (computer fonts) to reproductions of Michaelangelo paintings -- are created by the simple process of calculated placement of one or more of these three types of pixels. In the same way, the vast and seemingly limitless variety of materials -- ranging from earth to air to fire to water, and including solid metals (iron), liquid metals (mercury), solid liquids (glass), and human DNA, to name a randomly chosen few -- are created by the simple process of joining one or more of the basic quantum units in a variety of combinations.
Thus, for example, we think of helium as the gas we use to blow up a balloon and
make it fly away; we think of plutonium as the radioactive element which powers
atomic bombs. These elements appear to be completely different materials; however,
the only difference between helium (He) and plutonium (Pu) is the number of protons,
neutrons and electrons in each, and their arrangement in the respective atoms.
So we see in the the computer pixel an example of how
we can create a vast and limitless variety of information displays using a relatively few basic
elements, changing only their arrangement. We also have an example of how discrete, individual
elements can be "blurred together" by perception, even while they remain completely separate in
fact. It is this perceptual blurring that creates both the variety of the display, and the impression of
smooth continuity. At this level of analysis, the smoothness, the continuity, and the information
content of the display itself is "illusion"; the green, red, and blue dots are "reality."
What is a pixel? By its nature, a pixel is the product of a calculation. The computer's
programming instructs the hardware that, upon such-and-such conditions, it should fire its electron
beam at a particular point on the monitor's screen. Where the beam hits, the fluorescent coating of
the monitor screen glows, and this is perceived by the user as a dot on the screen.
The reason the computer would do such a thing is to display information to the user who is sitting at the computer's monitor. What information? Any information the computer has in its memory. The information could be words, in which case it would use the pixels to form letters, words and sentences. The information could be pictures, in which case the pixels would form images. The information could be mathematical relationships, in which case the pixels might form wavy lines that shape up into graphs (like the sine wave graphs we have used as illustrations). Whatever information the computer has, it may use the pixels to display.
What happens to the pixel -- or the word or the image or the graph -- when you turn off the monitor? In one sense, it ceases to exist; that is, you no longer see the pixel on the screen or anywhere else, and you will not find it no matter how hard you look. In another sense, the pixel continues to exist just as much as it ever did; that is, it still exists as a product of the programming, a potential dot on the screen which will reappear when you turn on the monitor. In this sense, the pixel is not so much a dot as it is the mathematical formula or algorithm that instructs the computer where to place dots when called upon to do so. To the computer, the important thing is the information. The pixel is only a way to display the information to the user.
Of course, to you, the user, the information itself is quite useless without the pixel to display the information. Imagine that a brilliant computer scientist has devised a program which will answer the questions of how to produce a just and lasting peace for the world, and how to produce food, shelter and uplifting entertainment in such abundance that no person will ever lack for anything. Now imagine further that the program is run on a computer, and the computer produces the answers -- but there is no monitor to display the answer. No monitor, no sound, no printer, no ticker tape readout, no nothing -- in short, no way for the computer to display the answer to any user. To obtain such answers, we might be willing to take the computer apart diode by diode; but we would disassemble the entire computer without ever discovering the answer, because the internal state of the machinery would not reveal anything about the programming or the results of the computer's calculations, i.e., the answers.[7] To the conventional computer, the answer has been produced and its job is done; it is up to the user to connect and turn on the monitor. To you, this state of affairs is no different from having no answer at all.
Which is more "real" -- the formula (the programming), or the dots displayed on your monitor? Which is more useful? Which is more fundamental to the overall operation of the computer? These are meant as rhetorical questions. Plainly, if we think of the computer as a machine that processes information for the benefit of the user, then the programming and the display are equally important. We would never be able to understand how a computer works and what it does by studying only the pixels that appear on the monitor screen. Indeed, if we focused exclusively on the pixels, and thought of the pixels as the only thing that was "real," we would surely end up completely baffled by the comings and goings of these little dots. We could coin a new cliché -- instead of "She can't see the forest for the trees," we could say, "She can't see the programming for the pixels."
Pixels -- whether displayed on a monitor or printed on paper -- are the "particles" of a computer operation. In one sense, they are and always will remain just little dots, meaningless in themselves. In another sense, they are the method by which the computer conveys its information to the user according to the agreed conventions of human perception. In a final sense, they are the products of the computer's calculations, determined by the programming, existing as "thoughts" in the computer regardless of whether they are displayed to the user.
Location property of pixel unit (x,y)
Brightness property of red pixel within pixel unit (rb)
Brightness property of green pixel within pixel unit (gb)
Brightness property of blue pixel within pixel unit (bb)Using these properties as our complete description of the pixel unit, we can say that the definition of a pixel unit is as follows: a "pixel unit" is a collection of three pixels located at coordinates x,y, consisting of a red pixel with brightness rb, a green pixel with brightness gb, and a blue pixel with brightness bb. This will be our formula for a pixel unit. We can now describe every one of the approximately 24.5 million pixel units on the monitor screen with just one formula, and we have used only 35 words. And we can now describe any individual pixel unit among these 24.5 million pixels using just 5 numbers: the x coordinate, the y coordinate, and the brightness of the red, green, and blue pixels (rb, gb, and bb).
In the simple algebra of computer programming, these "properties" are the variables in the formula. Think of it as a fill-in-the-blanks exercise:
The pixel unit is located at coordinates ___, ___, consisting of a red pixel with brightness ___, a green pixel with brightness ___, and a blue pixel with brightness ___.
The computer can -- and usually does -- set limits on what you fill in. The most obvious limit in the above example is that you must fill in a number. That is, you may not fill in the blank with a letter, the name of your dog, a mystical runic symbol, or a Michaelangelo painting. My computer also insists that the number must be a whole number, i.e., 0, 1, 2, 3, 4, . . ., not 1.7695 or any other decimal or fraction. Also, the number must be a positive number, because the computer does not know what to make of a negative value for any of these numbers. ("Take away some red? B-but I didn't put any red there in the first place!?") Furthermore, the computer will usually define a range for the value of the variable. The graphics programs I use limit the range of red, green, and blue to whole, positive numbers between 0 and 65,535.[8]
As a practical matter, the x and y coordinates ordinarily will be limited by the size of the monitor and its resolution. In the example of my computer monitor, the x coordinate would have to be between 0 and 6,400 to fit on the screen, and the y coordinate between 0 and 3,840, because there are only that number of pixels across and down. However, the computer doesn't really care whether the pixel fits on the screen or not; it would be just as happy to keep track of a pixel located several feet to the right of the computer monitor. So, for example, if I entered an x coordinate with a value of 9,600, it would be located "offscreen," about five inches to the right of my monitor's screen. This is not a problem for the computer. The computer will treat such an offscreen pixel on an equal basis with all the onscreen pixels; however, such a pixel simply does not get displayed. If I sprang for a monitor that was fifteen inches wide, the computer would display the pixel at the far right edge. As far as the computer is concerned, it's up to me, the user. The "hypothetical" pixel which would be displayed if I bought a bigger monitor remains part of the computer's memory in just the same way as the "real" pixel which can be and, therefore, is displayed.
So we see that, in computer terms, a "property" may be thought of as the value of a variable needed to complete the description or definition of a unit of information such as a pixel. In other words, the number that the computer uses to fill in a required blank. And we see that this way of operating allows for a great deal of flexibility in the way that the computer can choose to handle any given property -- in particular, whether or not it is displayed -- without restricting the underlying programming. Finally, we see that this way of dealing with properties is an efficient way of handling huge amounts of information -- vast numbers of "particles" which are both identical in definition and individually unique in value -- using simple definitions and instructions.
Building a model of the universe. From the parts described in this chapter, we can begin to build a model of the universe as though it were run by a cosmic computer. Quantum waves behave much more like waves generated by a computer than like physical waves. Quantum properties are much more like variables in a computer's formulas than like physical properties. And quantum "particles" are very much like the evanescent dots on your computer screen which are here when you need them and tucked away in memory when you don't.
In the next few chapters, we will look at some of the other oddities of quantum mechanics, and try to draw some analogies to equivalent operations of the computer. In this way, we will begin to imagine how the puzzles of quantum mechanics might be compared to something that we can understand, something with which we have some experience. Something like a computer.
| 1. [Back] | The theoretical physicist Michio Kaku deals with the problem in a brief footnote, concluding that, "over the decades we have simply gotten used to the idea that light can travel through a vacuum even if there is nothing to wave." M. Kaku, Hyperspace (Oxford University Press, New York, 1994), at 8n. |
| 2. [Back] | There are actually two basic ways of generating "synthesized" sound. In one method, the computer begins and ends with formulas, as in the example above. In another method, the process begins by "sampling" a live sound source: the engineer actually puts a microphone near a piano, or a saxophone, or a barking dog (avant garde music), or whatever. Every distinctive sound source will have a distinctive sound, which is to say, a distinctive wave pattern. The recorded sound wave pattern is then converted into a string of numbers, and the computer takes it from there. Sampling live sound sources has the advantage of giving the electronic composer the exact sound for which he or she is searching without a lot of fiddling (no pun intended), usually when the intention is to "recreate," or copy, the original instrumental sound. Because I am interested in what a computer can do without ever leaving its digital world, I focus on the first method of sound synthesis. |
| 3. [Back] | From the abstract to the 1997 senior paper of Steven Cason, a student at the
University of California at Santa Barbara, which used to be posted on the web
but, alas, no longer. See "Holography
without photography", Thad G. Walker, Am. J. Phys. 67,
783, September 1999. http://www-atoms.physics.wisc.edu/papers%5Cholo.pdf See also E. Allaria, et al., Digital holography at 10.6 microns, Optics Communications 215 (2003) 257–262, http://www.ino.it/~stefanob/digital_holography.pdf |
| 4. [Back] | National Institute of Applied
Optics, Florence, Italy, http://www.ino.it/UNI3/1.htm |
| 5. [Back] | These are the primary colors for mixing light. The computer monitor mixes the light produced by the fluorescent glowing dots. Mixing pigments for painting or printing is a different set of calculations because pigments absorb colors; therefore, the primary colors for mixing pigments are "opposite": cyan (green-blue), magenta (blue-red), and yellow. These are the colors used by the computer when it is displaying information to a color printer instead of to a monitor. |
| 6. [Back] | This description simplifies computer graphics somewhat. However, the various schemes to improve the display could be achieved by increasing the number of dots, or pixels, per inch. |
| 7. [Back] | The indefatigable computer scientist might suggest separately testing each and every memory location in the computer to obtain its binary (0 or 1) state, and then spending the next few million years reconstructing all of the information contained in the computer. I rule out this possibility, because testing the memory locations is simply another way -- a very tedious way -- of obtaining a display of the information. |
| 8. [Back] | The number 65,535 is not completely arbitrary. Recall that most computer operations are performed in binary form, where there are only two numbers, 0 and 1. For this reason, most of the basic limits of the computer come in multiples of 2, and particularly in 2 multiplied by itself some number of times. Two multiplied by itself 12 times (or, "2 raised to the 12th power") equals 65,536 (212 = 65536). Since 0 is a valid number for the computer, the number 65,535 actually represents 65,536 possibilities. |
The Reality Programby Ross Rhodes
9/15/02 The Notebook of Philosophy & Physics |