Natural time. Let us think about time. I will begin by asking a question: Is time a
continuously flowing stream, in which the past smoothly evolves into the present, which smoothly
evolves into the future? Or is time a series of still shots, like at the movies, each one flashing by so
rapidly that it only seems like changes are smooth and continuous? The question has been asked
for some 2,500 years, and there has never been any clear answer. Scientifically, the question is
difficult to answer because there is not much evidence one way or the other. So the question has
been placed on a kind of scientific back burner which is very far back indeed, and scientists
generally make the working assumption that time is continuous, just as it appears to be. This is not
to say that the nature of time is irrelevant, or that it has no bearing on current scientific theories.
On the contrary, some of the signature characteristics of quantum mechanics can be understood
more easily if we assume that time is not continuous.
The basic argument is primarily associated with an early Greek philosopher, Zeno of Elea (c. 450 B.C.). Zeno posed a famous series of paradoxes about the nature of motion, which is the change of a body's position in space over a period of time. His purpose, apparently, was to defend the position of his mentor, Parmenides, that time and space were continuous. This position was challenged by the "atomists," represented by Democritus of Abdera, among others, who maintained that all things were composed of discrete, indivisible units. However, as Zeno's paradoxes have been analyzed and re-analyzed over the centuries, the philosophical results have not always seemed to support the view that space and time are continuous. This may be due to the fact that we do not have Zeno's original arguments; our best source is from Aristotle, writing much later, who thought the paradoxes ridiculous and wrote them down mostly to show how foolish they were.
In its most familiar form, Zeno's paradox analyzes motion to determine whether space is continuous. He imagines the swift Achilles trying to run some distance to reach a finish line. The philosophical paradox is this: in order to get to the line, Achilles first must get half-way to the line; in order to get half-way, he first must get half-way to the half-way point; in order to get to that point, he must first get half-way there; and so on to infinity. Achilles always has one more half-way point to reach before he can get to the finish line. Because the number of such halfway points is logically infinite (if space is continuous), and because Achilles cannot travel through an infinite number of points in a finite amount of time (say, the lifetime of Achilles), therefore, he can never get to the finish line. In fact, he can never move at all because, by this logical argument, there always will be an infinite number of sub-points between any two points.
The philosophical lesson to be drawn from this absurd result has often seemed unsatisfying. Logic seems to dictate that if space is infinitely divisible -- which is to say, if space is continuous -- then Achilles cannot move. But we see that Achilles actually can move and that he does so all the time (as do we all). Therefore, space logically cannot be infinitely divisible, which is to say that space must be composed of discrete, indivisible units, like atoms of space. There must be some smallest distance at which there is no half-way point to the next point. The logic dictates that there has to come a point at which there is no more length; at which the movement from one place to another place does not involve passing through any intermediate place. This solution is resisted, with philosophers frequently stumbling on the question of what lies between the two points that are adjacent but irreducible? By definition, there would be nothing between these two points, but the mind reels at the concept of actual nothingness -- a nothingness that is not air, not a vacuum, not even empty space. Not even nothing.
Because motion also involves the concept of time, Zeno proposed further paradoxes
examining whether time is continuous, like a conventional watch's sweeping hands, or
discontinuous, like the digital watch's abruptly changing numbers. In one such paradox, Zeno
imagined two lines which were exactly three points long (according to the theory that space is
composed of a series of smallest, irreducible points1). Zeno then labeled the three points at the
beginning, middle and end of each line, and laid the two lines next to each other so that the points
lined up.

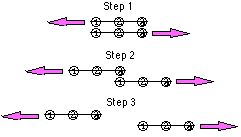
Apparently, Zeno and his followers thought this result ridiculous (Aristotle, at least, thought so), because it implied that the end points were never opposite the middle points -- that they had jumped right to the end, going from Point 1 to Point 3, without passing Point 2. This was long assumed to be logically impossible, in the same way that Achilles's inability to move was logically impossible, and so this paradox was long used to argue as a philosophical matter that space and time cannot be "atomized," but must be continuous. However, if one were to accept that a "particle" can jump from place to place without passing through intervening space, then the intellectual quandary disappears, and this paradox becomes an argument that space and time may come in discrete, indivisible units -- "quantums" of space and time.
With the advent of quantum mechanics, this concept of "jumping" has become commonplace, regardless of whether it agrees with our common sense. It must be admitted that the concept of "jumping" in the manner foreseen by Zeno can no longer be considered scientifically illogical, ridiculous, or even unusual. As a result, the philosophical problem that stymied Zeno and his followers is removed, and we may analyze his paradox with a fresh mind.
If we are to assume that time is continuous, then the points on Zeno's hypothetical line can never move at all because, as with Achilles, there will always be an infinite series of "instants" requiring motion from point #1 to point #2. On the other hand, if we are to assume that time is "atomized" or "quantized," then there is no difficulty once the "common sense" objection to jumping is removed. By this logic, the philosophical argument appears to favor atomized, or quantized time.
The idea that time is a series of moments rather than an ever-flowing stream has played a part in other philosophical and religious discussions since the time of Zeno. G. H. Whitrow, in The Natural Philosophy of Time (Clarendon Press, Oxford (2nd ed. 1980)), surveys a number of such debates, ranging from early Buddhist sects to Jewish, Christian and Islamic scholars in the Middle Ages. Later, Descartes and some of his contemporaries arrived at the conclusion that time is composed of discontinuous instants, driven in part by their religious views and in part by their sense of physical logic.
So the quantization of space and time is at once logically plausible (if not compelled), historically precedented, and scientifically valid. We may, therefore, consider how this proposition which seems to go against our everyday experience might impact on our model of the universe -- in the same way that we must consider how phenomena such as the measurement effect and the uncertainty principle (which are equally if not more bizarre to contemplate) must be incorporated into any valid model of the universe.
Computer time. In a computer, time is not continuous. Computer time consists of one tick after another of some clock which controls its operations. This is because all computer operations occur one at a time, one after the other, in a step-by-step manner. This is true of all computers that presently exist, and is probably basic to the nature of a computer, at least as we know it. There do not appear to be any satisfactory theoretical models that would allow a computer to do anything else but perform one operation at a time.2
Natural space. In looking at time, we have touched on the debate over whether space is
continuous or quantized. Regardless of how it is viewed, scientific analysis has found it useful
conceptually to divide all space into coordinate grids. That is, we can graph points in space
according to their relative positions along three lines, corresponding to the three spatial dimensions
(height, width, and depth).
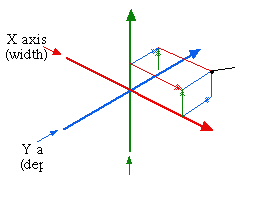
It doesn't matter where we place the zero point, i.e., the spot where the three axes come together. In fact, we can use more than one grid to describe the same point in space, if that suits our purposes. Think of two air traffic controllers, one at New York's LaGuardia airport and one at Chicago's O'Hare airport. If both wanted to track an airplane flying over Ohio, they could either choose a common coordinate system, say, based at Washington's Dulles airport, or they could choose separate coordinate systems based at their own airports. If they choose a common coordinate system, the three numbers describing the plane's position over Ohio will be the same for both controllers, because all distances are being measured from the same spot in Washington, D.C. If they choose to measure distances from their own separate airports, their numbers will be completely different. However, in either case, the airplane is exactly where it is over Ohio. Only the coordinate system, or the frame of reference, has changed.
You can see that we can choose either to view this graphing of coordinates as quantized (by allowing only whole numbers for coordinates), or as continuous (by allowing fractional or decimal numbers as coordinates). Coordinate systems were developed by Descartes as a way of imposing an artificial order on the vastness of nature to aid in mathematical analysis. The hypothetical grid can be of any size or scale, depending on the analyst's need for accuracy. For example, if the air traffic controllers' coordinate system used only distances in whole miles, they would be able to locate the airplane only to within a region of one cubic mile, which might not be sufficient to avoid collisions. They could just as easily use a grid with divisions of 1/10th of a mile, or inches, or nanometers. As a practical matter, the scale will be limited by the accuracy of the radar or other positioning devices being used to locate the airplane; other than that, it is simply a matter of using larger and larger numbers to represent the same distance in smaller and smaller units. Regardless of the scale, the coordinate grid still needs only three such numbers.
Computer space. Computer imaging has adopted the Cartesian coordinate system (i.e., the coordinate grid system originated by Descartes) to track its placement of pixels in either two or three dimensions. The principle difference between a computer's operation and the air traffic controller's operation is that the computer's coordinate grid is necessarily quantized. This mean's that the computer's grid will be exact, because the numbers themselves are being used to place the dots. The air traffic controller's grid, on the other hand, is meant only as a mathematical approximation of the assumed continuous reality. The air traffic numbers are being used to describe a fact (the location of the airplane) which exists regardless of whether the air traffic controllers are aware of it or can measure it.
Quantum space. Quantum theory assumes that space and time are continuous. This is simply an assumption, not a necessary part of the theory.3 However, this assumption has raised some difficulties when performing calculations of quantum mechanical phenomena. Chief among these is the recurring problem of infinities.
In quantum theory, all quantum units which appear for the purpose of measurement are conceived of as dimensionless points. These are assigned a place on the coordinate grid, described by the three numbers of height, depth, and width as we have seen, but they are assigned only these three numbers. If you consider any physical object, it will have some size, which is to say it will have its own height, width, and depth. If you were to exactly place such a physical object, you would have to take into account its own size, and to do so you would have to assign coordinates to each edge of the object. For example, suppose you are trying to locate an airplane using a coordinate grid. You might well start by finding the three numbers which exactly place the center of the airplane (say, row 18, seat E) at some point in space. But, then you are left with the question of how big is the airplane? What sort of margin do we have to leave around this central point to avoid having another airplane fly into its tail or wingtip? The answer will vary depending on whether the airplane is a small private plane, or a Boeing 747, or a military transport. Consequently, you must also give coordinates for each wingtip, each tail fin, the nose piece, and any other projections. This runs up a lot of numbers. It is easier for the air traffic computers to plot just a single point, and then leave a wide berth around it.
In the same way, when physicists consider quantum units as particles, there does not seem to be any easy way to determine their outer edges, if, in fact, they have any outer edges.4 Accordingly, quantum "particles" are designated as simple points, without size and, therefore, without edges. The three coordinate numbers are then sufficient to locate such a pointlike particle at a single point in space.
The difficulty arises when the highly precise quantum calculations are carried out all the way down to an actual zero distance (which is the size of a dimensionless point -- zero height, zero width, zero depth). At that point [sic], the quantum equations return a result of infinity, which is as meaningless to the physicist as it is to the philosopher. This result gave physicists fits for some twenty years (which is not really so long when you consider that the same problem had been giving philosophers fits for some twenty-odd centuries). The quantum mechanical solution was made possible when it was discovered that the infinities disappeared if one stopped at some arbitrarily small distance -- say, a billionth-of-a-billionth-of-a-billionth of an inch -- instead of proceeding all the way to an actual zero. One problem remained, however, and that was that there was no principled way to determine where one should stop. One physicist might stop at a billionth-of-a-billionth-of-a-billionth of an inch, and another might stop at only a thousandth-of-a-billionth-of-a-billionth of an inch. The infinities disappeared either way. The only requirement was to stop somewhere short of the actual zero point. It seemed much too arbitrary. Nevertheless, this mathematical quirk eventually gave physicists a method for doing their calculations according to a process called "renormalization," which allowed them to keep their assumption that an actual zero point exists, while balancing one positive infinity with another negative infinity in such a way that all of the infinities cancel each other out, leaving a definite, useful number.5
In a strictly philosophical mode, we might suggest that all of this is nothing more than a revisitation of Zeno's Achilles paradox of dividing space down to infinity. The philosophers couldn't do it, and neither can the physicists. For the philosopher, the solution of an arbitrarily small unit of distance -- any arbitrarily small unit of distance -- is sufficient for the resolution of the paradox. For the physicist, however, there should appear some reason for choosing one small distance over another. None of the theoretical models have presented any compelling reason for choosing any particular model as the "quantum of length." Because no such reason appears, the physicist resorts to the "renormalization" process, which is profoundly dissatisfying to both philosopher and physicist. Richard Feynman, who won a Nobel prize for developing the renormalization process, himself describes the procedure as "dippy" and "hocus-pocus."6 The need to resort to such a mathematical sleight-of-hand to obtain meaningful results in quantum calculations is frequently cited as the most convincing piece of evidence that quantum theory -- for all its precision and ubiquitous application -- is somehow lacking, somehow missing something. It may be that one missing element is quantized space -- a shortest distance below which there is no space, and below which one need not calculate. The arbitrariness of choosing the distance would be no more of a theoretical problem than the arbitrariness of the other fundamental constants of nature -- the speed of light, the quantum of action, and the gravitational constant. None of these can be derived from theory, but are simply observed to be constant values. Alas, this argument will not be settled until we can make far more accurate measurements than are possible today.
Quantum time. If space is quantized, then time almost surely must be quantized also. This relationship is implied by the theory of relativity, which supposes that time and space are so interrelated as to be practically the same thing. Thus, relativity is most commonly understood to imply that space and time cannot be thought of in isolation from each other; rather, we must analyze our world in terms of a single concept -- "space-time." Although the theory of relativity is largely outside the scope of this book, the reader can see from Zeno's paradoxes how space and time are intimately related in the analysis of motion. For the moment, I will only note that the theory of relativity significantly extends this view, to the point where space and time may be considered two sides of the same coin.
The idea of "quantized" time has the intellectual virtue of consistency within the framework of quantum mechanics. That is, if the energies of electron units are quantized, and the wavelengths of light are quantized, and so many other phenomena are quantized, why not space and time? Isn't it easier to imagine how the "spin" of an electron unit can change from up to down without going through anything in the middle7 if we assume a quantized time? With quantized time, we may imagine that the change in such an either/or property takes place in one unit of time, and that, therefore, there is no "time" at which the spin is anywhere in the middle (just as there is no "time" at which Zeno's points are directly opposite each other). Without quantized time, it is far more difficult to eliminate the intervening spin directions.
Nevertheless, the idea that time (as well as space) is "quantized," i.e., that time comes in individual units, is still controversial. The concept has been seriously proposed on many occasions, but most current scientific theories do not depend on the nature of time in this sense. About all scientists can say is that if time is not continuous, then the changes are taking place too rapidly to measure, and too rapidly to make any detectable difference in any experiment that they have dreamed up. The theoretical work that has been done on the assumption that time may consist of discontinuous jumps often focuses on the most plausible scale, which is related to the three fundamental constants of nature -- the speed of light, the quantum of action, and the gravitational constant. This is sometimes called the "Planck scale," involving the "Planck time," after the German physicist Max Planck, who laid much of the foundation of quantum mechanics through his study of minimum units in nature. On this theoretical basis, the pace of time would be around 10-44 seconds. That is one billionth-of-a-billionth-of-a-billionth-of-a-billionth of a second. And that is much too quick to measure by today's methods, or by any method that today's scientists are able to conceive of, or even hope for.8
Since calculus was introduced in the late 1600s, it has been possible to assume that an infinity actually exists while using mathematics to "approach" the infinity in a sufficiently close approximation to achieve a definite result.9 With these mathematical tools well in hand, physics has never been forced to choose between continuous time and quantized time. Moreover, as with space, there has never been any compelling physical argument for choosing any particular unit of time as the minimum quantum. Whatever unit was chosen as the quantum of time would seem to be completely arbitrary.
And yet, physics continues to be puzzled by the fundamental fact of the quantum. While the very essence of quantum mechanics lies in the step-like (as opposed to ramp-like) nature of innumerable phenomena; and while the mathematical tools are available to incorporate this essence into a coherent scheme; still, there is no good explanation of why nature should divide itself up according to these whole numbers, and why there should be nothing in between. As mentioned earlier, these riddles can be resolved if we assume instead that time is not continuous, and that the quantization of time causes the quantization of physical properties. How would this work? If we assume that the "physical" processes occur in one unit of time, then there is no "time" at which the process is in transition. At the first time step, the "physical" process is in state 1; at the next time step, the "physical" process is in state 2. There is no "time" at which the "physical" process is in state 1-1/2.
Mixing philosophy, science, time, and space. We see that the branch of physics known as relativity has been remarkably successful in its conclusion that space and time are two sides of the same coin, and should properly be thought of as a single entity: space-time. We see also that the philosophical logic of Zeno's paradoxes has always strongly implied that both space and time are quantized at some smallest, irreducible level, but that this conclusion has long been resisted because it did not seem to agree with human experience in the "real world." Further, we see that quantum mechanics has both discovered the ancient paradoxes anew in its mathematics, and provided some evidence of quantized space and time in its essential experimental results showing that "physical" processes jump from one state to the next without transition. The most plausible conclusion to be drawn from all of this is that space and time are, indeed, quantized. That is, there is some unit of distance or length which can be called "1," and which admits no fractions; and, similarly, there is some unit of time which can be called "1," and which also admits no fractions.
Although most of the foregoing is mere argument, it is compelling in its totality, and it is
elegant in its power to resolve riddles both ancient and modern. Moreover, if we accept the
quantization of space and time as a basic fact of the structure of our universe, then we may go on to
consider how both of these properties happen to be intrinsic to the operations of a computer.
| 1 | For the paradox, it is not strictly necessary to imagine that the space, and therefore the labeled points, are themselves quantized. We could simply take three arbitrary points at the beginning, middle, and end of the lines. In that set up, we would simply define the points as being separated by whatever distance the line could move in one step of time. | Back |
| 2 | Parallel processing, by which computers use many sub-computers to work different parts of the same problem, are able to reduce the bottleneck. Although, in a sense, this arrangement allows the computing system to perform more than one operation at a time, it remains true that each computing unit, i.e., each processor, operates according to the step-by-step process. See R. Penrose, The Emperor's New Mind, at 398. | Back |
| 3 | In conventional quantum analysis, the jumps are associated with "eigenstates," which may be thought of as periodically recurring harmonics in the mathematical "waves." | Back |
| 4 | The closest thing to a definition of the "size" of a quantum unit is its "wavelength." This is, roughly speaking, the range of space in which the quantum unit might turn up when we ask for its location. However, this cannot be equated with, say, the diameter of a billiard ball. | Back |
| 5 | R. Feynman, QED, at 127-28. | Back |
| 6 | Id. at 128. | Back |
| 7 | This phenomenon is used as the basis for the "stem direction" property of our hypothetical "quantum grapes", discussed elsewhere. | Back |
| 8 | Other theoretical models begin with certain quantum processes to arrive at a minimum time unit that is considerably longer, but still only about a billionth-of-a-billionth of a second. It is a comfort to know that we will never be caught in between moments of time. | Back |
| 9 | Mathematicians periodically assert that Zeno's paradoxes have been "solved" using these mathematical tools. See, e.g., Wm. I. McLaughlin, "Resolving Zeno's Paradoxes," Sci. Am. Nov. 1994, pp. 84 et seq. In that article, the author uses a concept of "infinitessimals" simply to stop counting at a "nonstandard" number which is conveniently defined as greater than zero but smaller than any number we can imagine. The conclusion appears straightforward: "it is clear that the points of space or time marked with concrete numbers are but isolated points." Id. at 87. The author goes on to assert that there is lots of stuff in between the points, but that everything in between is, by definition, unimaginable and, therefore, drops out of the math. If we remove this qualifying conjecture (which recalls the Sophist school), we are left with space and time consisting of isolated, concrete points, which is the only way anybody has been able to resolve Zeno's paradoxes. | Back |
The Reality Programby Ross Rhodes
9/15/02 The Notebook of Philosophy & Physics |